Copyright (c) 2017
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
FITNESS FOR A PARTICULAR PURPOSE AND NON INFRINGEMENT. IN NO EVENT SHALL THE
AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN
THE SOFTWARE.
Bug reports: miguel.luque.easp at juntadeandalucia.es
. set more off . use https://stats.idre.ucla.edu/stat/examples/asa2/whas100, clear . label define status 0 "alive" 1 "dead" . label value folstatus status . label define gender 0 "male" 1 "female" . label value gender gender . label var addate "Admission date" . label var foldate "Follow up date" . label var hosstay "Length of Hospital Stay in days" . label var foltime "Follow Up Time" . label var folstatus "Vital Status" . describe Contains data from https://stats.idre.ucla.edu/stat/examples/asa2/whas100.dta obs: 100 vars: 9 5 Nov 2007 15:59 size: 2,700 ---------------------------------------------------------------------------------------------- storage display value variable name type format label variable label ---------------------------------------------------------------------------------------------- id byte %8.0g addate str8 %9s Admission date foldate str8 %9s Follow up date hosstay byte %8.0g Length of Hospital Stay in days foltime int %8.0g Follow Up Time folstatus byte %8.0g status Vital Status age byte %8.0g gender byte %8.0g gender bmi float %9.0g ---------------------------------------------------------------------------------------------- Sorted by: . list, sep(0) noobs +------------------------------------------------------------------------------------+ | id addate foldate hosstay foltime folsta~s age gender bmi | |------------------------------------------------------------------------------------| | 1 3/13/95 3/19/95 4 6 dead 65 male 31.38134 | | 2 1/14/95 1/23/96 5 374 dead 88 female 22.6579 | | 3 2/17/95 10/4/01 5 2421 dead 77 male 27.87892 | | 4 4/7/95 7/14/95 9 98 dead 81 female 21.47878 | | 5 2/9/95 5/29/98 4 1205 dead 78 male 30.70601 | | 6 1/16/95 9/11/00 7 2065 dead 82 female 26.45294 | | 7 1/17/95 10/15/97 3 1002 dead 66 female 35.71147 | | 8 11/15/94 11/24/00 56 2201 dead 81 female 28.27676 | | 9 8/18/95 2/23/96 5 189 dead 76 male 27.12082 | | 10 7/22/95 12/31/02 9 2719 alive 40 male 21.78971 | | 11 10/11/95 12/31/02 6 2638 alive 73 female 28.43344 | | 12 5/26/95 9/29/96 11 492 dead 83 male 24.66175 | | 13 5/21/95 3/18/96 6 302 dead 64 female 27.46412 | | 14 12/14/95 12/31/02 10 2574 alive 58 male 29.83756 | | 15 11/8/95 12/31/02 7 2610 alive 43 male 22.95776 | | 16 10/8/95 12/31/02 5 2641 alive 39 male 30.10881 | | 17 10/17/95 5/12/00 6 1669 dead 66 male 31.99738 | | 18 10/30/95 1/5/03 9 2624 dead 61 male 30.7142 | | 19 12/10/95 12/31/02 6 2578 alive 49 male 25.69548 | | 20 11/23/95 12/31/02 5 2595 alive 53 female 30.12017 | | 21 10/5/95 2/5/96 6 123 dead 85 male 18.41038 | | 22 11/5/95 12/31/02 8 2613 alive 69 female 37.60097 | | 23 9/9/95 10/22/97 4 774 dead 54 male 28.97529 | | 24 9/9/95 3/13/01 14 2012 dead 82 male 19.90095 | | 25 12/15/95 12/31/02 4 2573 alive 67 female 28.32237 | | 26 12/3/95 1/19/01 11 1874 dead 89 female 23.43605 | | 27 10/18/95 12/31/02 2 2631 alive 68 male 26.44693 | | 28 3/16/95 6/4/00 7 1907 dead 78 male 28.20595 | | 29 10/25/95 4/15/97 5 538 dead 56 male 24.11997 | | 30 10/6/95 1/18/96 4 104 dead 85 female 36.71647 | | 31 9/3/95 9/9/95 4 6 dead 72 male 27.97907 | | 32 6/30/95 5/1/99 5 1401 dead 50 male 20.363 | | 33 7/22/95 12/22/02 8 2710 dead 81 female 28.64898 | | 34 9/17/95 1/5/98 4 841 dead 85 female 20.17772 | | 35 3/21/97 8/16/97 6 148 dead 84 female 23.6187 | | 36 2/23/97 12/31/02 12 2137 alive 75 male 23.67519 | | 37 1/1/97 12/31/02 16 2190 alive 61 male 23.4314 | | 38 1/18/97 12/31/02 5 2173 alive 48 male 33.4511 | | 39 1/19/97 4/25/98 8 461 dead 83 female 19.57068 | | 40 3/18/97 12/31/02 10 2114 alive 82 male 25.82748 | | 41 2/3/97 12/31/02 4 2157 alive 62 male 30.86625 | | 42 5/17/97 12/31/02 5 2054 alive 39 male 24.21079 | | 43 3/8/97 12/31/02 5 2124 alive 45 male 31.66439 | | 44 2/23/97 12/31/02 4 2137 alive 65 male 26.22085 | | 45 6/14/97 1/5/03 18 2031 dead 76 female 32.41986 | | 46 7/7/97 12/31/02 9 2003 alive 77 female 24.56345 | | 47 4/27/97 12/31/02 9 2074 alive 68 male 21.3055 | | 48 5/15/97 2/13/98 7 274 dead 73 male 26.45678 | | 49 7/26/97 12/31/02 4 1984 alive 64 male 27.97977 | | 50 7/17/97 12/31/02 6 1993 alive 80 male 36.02333 | | 51 9/9/97 12/31/02 7 1939 alive 84 female 22.31424 | | 52 6/19/97 9/3/00 4 1172 dead 43 female 25.33148 | | 53 8/20/97 11/17/97 3 89 dead 87 female 18.77718 | | 54 8/28/97 1/3/98 7 128 dead 70 female 18.60004 | | 55 9/9/97 12/31/02 17 1939 alive 80 male 25.50204 | | 56 9/1/97 9/15/97 11 14 dead 64 female 24.41255 | | 57 9/3/97 6/10/00 5 1011 dead 59 female 29.85998 | | 58 9/24/97 10/30/01 6 1497 dead 92 male 24.3664 | | 59 9/19/97 12/31/02 3 1929 alive 51 male 34.77034 | | 60 4/17/97 12/31/02 1 2084 alive 41 male 27.26234 | | 61 10/21/97 2/5/98 6 107 dead 90 male 24.78423 | | 62 10/2/97 12/27/98 4 451 dead 83 male 21.80987 | | 63 1/8/97 12/31/02 3 2183 alive 61 male 27.36909 | | 64 11/11/97 12/31/02 7 1876 alive 64 male 26.22085 | | 65 11/7/97 5/31/00 3 936 dead 82 male 26.88683 | | 66 4/20/97 4/18/98 5 363 dead 91 female 27.61844 | | 67 6/18/97 5/1/00 5 1048 dead 48 male 31.58373 | | 68 10/29/97 12/31/02 12 1889 alive 63 male 23.33267 | | 69 4/29/97 12/31/02 5 2072 alive 81 male 28.35006 | | 70 11/8/97 12/31/02 7 1879 alive 52 male 32.63621 | | 71 11/17/97 12/31/02 4 1870 alive 65 male 31.95113 | | 72 11/28/97 12/31/02 5 1859 alive 74 male 25.01782 | | 73 5/19/97 12/31/02 5 2052 alive 62 male 30.22827 | | 74 12/11/97 12/31/02 4 1846 alive 60 female 29.28812 | | 75 5/10/97 12/31/02 7 2061 alive 71 male 32.32407 | | 76 10/6/97 12/31/02 3 1912 alive 73 male 31.47445 | | 77 12/21/97 12/31/02 5 1836 alive 43 male 28.59188 | | 78 11/22/97 3/16/98 7 114 dead 80 male 33.36074 | | 79 10/31/97 2/4/02 7 1557 dead 72 male 21.80987 | | 80 6/28/97 12/27/00 5 1278 dead 57 male 23.57087 | | 81 12/21/97 12/31/02 3 1836 alive 80 female 28.35006 | | 82 10/2/97 12/31/02 6 1916 alive 76 male 28.03555 | | 83 9/14/97 12/31/02 3 1934 alive 53 male 24.21079 | | 84 9/25/97 12/31/02 10 1923 alive 44 male 32.60387 | | 85 12/2/97 1/15/98 3 44 dead 71 male 23.0563 | | 86 9/26/97 12/31/02 6 1922 alive 64 male 31.75016 | | 87 10/24/97 7/25/98 5 274 dead 86 male 21.10959 | | 88 11/27/97 12/31/02 7 1860 alive 72 female 25.23266 | | 89 4/12/97 3/23/02 4 1806 dead 73 female 22.86698 | | 90 2/15/97 12/31/02 6 2145 alive 85 female 26.05501 | | 91 10/22/97 4/22/98 5 182 dead 60 male 23.18023 | | 92 6/27/97 12/31/02 4 2013 alive 63 male 35.48949 | | 93 1/17/97 12/31/02 5 2174 alive 80 female 20.59809 | | 94 12/12/97 5/24/02 4 1624 dead 74 male 30.13206 | | 95 11/4/97 5/10/98 10 187 dead 79 female 16.78615 | | 96 11/4/97 12/31/02 4 1883 alive 48 female 32.11709 | | 97 12/24/97 4/19/02 3 1577 dead 32 female 39.93835 | | 98 11/26/97 1/27/98 8 62 dead 86 female 14.91878 | | 99 8/10/97 12/31/02 16 1969 alive 56 male 29.05295 | | 100 3/26/97 2/13/00 7 1054 dead 74 male 32.89087 | +------------------------------------------------------------------------------------+
. gen entry = date(addate, "MD19Y") . format entry %td . gen exit = date(foldate, "MDY", 2003) . format exit %td . stset exit, fail(folstatus==1) enter(time entry) origin(time entry) // Scale in days failure event: folstatus == 1 obs. time interval: (origin, exit] enter on or after: time entry exit on or before: failure t for analysis: (time-origin) origin: time entry ------------------------------------------------------------------------------ 100 total observations 0 exclusions ------------------------------------------------------------------------------ 100 observations remaining, representing 51 failures in single-record/single-failure data 150,540 total analysis time at risk and under observation at risk from t = 0 earliest observed entry t = 0 last observed exit t = 2,719 . stdescribe // In days failure _d: folstatus == 1 analysis time _t: (exit-origin) origin: time entry enter on or after: time entry |-------------- per subject --------------| Category total mean min median max ------------------------------------------------------------------------------ no. of subjects 100 no. of records 100 1 1 1 1 (first) entry time 0 0 0 0 (final) exit time 1505.4 6 1877.5 2719 subjects with gap 0 time on gap if gap 0 time at risk 150540 1505.4 6 1877.5 2719 failures 51 .51 0 1 1 ------------------------------------------------------------------------------ . stset exit, fail(folstatus==1) enter(time entry) origin(time entry) scale(365.25) // Scale i > n years failure event: folstatus == 1 obs. time interval: (origin, exit] enter on or after: time entry exit on or before: failure t for analysis: (time-origin)/365.25 origin: time entry ------------------------------------------------------------------------------ 100 total observations 0 exclusions ------------------------------------------------------------------------------ 100 observations remaining, representing 51 failures in single-record/single-failure data 412.156 total analysis time at risk and under observation at risk from t = 0 earliest observed entry t = 0 last observed exit t = 7.444216 . stdescribe // In years failure _d: folstatus == 1 analysis time _t: (exit-origin)/365.25 origin: time entry enter on or after: time entry |-------------- per subject --------------| Category total mean min median max ------------------------------------------------------------------------------ no. of subjects 100 no. of records 100 1 1 1 1 (first) entry time 0 0 0 0 (final) exit time 4.121561 .0164271 5.140315 7.444216 subjects with gap 0 time on gap if gap 0 time at risk 412.15606 4.121561 .0164271 5.140315 7.444216 failures 51 .51 0 1 1 ------------------------------------------------------------------------------ . stset foltime, fail(folstatus==1) scale(365.25) // Using the computed time failure event: folstatus == 1 obs. time interval: (0, foltime] exit on or before: failure t for analysis: time/365.25 ------------------------------------------------------------------------------ 100 total observations 0 exclusions ------------------------------------------------------------------------------ 100 observations remaining, representing 51 failures in single-record/single-failure data 412.156 total analysis time at risk and under observation at risk from t = 0 earliest observed entry t = 0 last observed exit t = 7.444216 . stdescribe // In years failure _d: folstatus == 1 analysis time _t: foltime/365.25 |-------------- per subject --------------| Category total mean min median max ------------------------------------------------------------------------------ no. of subjects 100 no. of records 100 1 1 1 1 (first) entry time 0 0 0 0 (final) exit time 4.121561 .0164271 5.140315 7.444216 subjects with gap 0 time on gap if gap 0 time at risk 412.15606 4.121561 .0164271 5.140315 7.444216 failures 51 .51 0 1 1 ------------------------------------------------------------------------------ . stvary // For multiple records failure _d: folstatus == 1 analysis time _t: foltime/365.25 subjects for whom the variable is never always sometimes variable | constant varying missing missing missing -------------+-------------------------------------------------------------- id | 100 0 100 0 0 addate | 100 0 100 0 0 foldate | 100 0 100 0 0 hosstay | 100 0 100 0 0 age | 100 0 100 0 0 gender | 100 0 100 0 0 bmi | 100 0 100 0 0 entry | 100 0 100 0 0 exit | 100 0 100 0 0
. sum foltime Variable | Obs Mean Std. Dev. Min Max -------------+--------------------------------------------------------- foltime | 100 1505.4 858.8992 6 2719 . gen yrfol = foltime/365.25 . sum yrfol Variable | Obs Mean Std. Dev. Min Max -------------+--------------------------------------------------------- yrfol | 100 4.121561 2.351538 .0164271 7.444216 . egen catyrfol = cut(yrfol), at(0,2,4,6,8) . tab catyrfol catyrfol | Freq. Percent Cum. ------------+----------------------------------- 0 | 25 25.00 25.00 2 | 11 11.00 36.00 4 | 50 50.00 86.00 6 | 14 14.00 100.00 ------------+----------------------------------- Total | 100 100.00 . stset catyrfol, fail(folstatus==1) failure event: folstatus == 1 obs. time interval: (0, catyrfol] exit on or before: failure ------------------------------------------------------------------------------ 100 total observations 25 observations end on or before enter() ------------------------------------------------------------------------------ 75 observations remaining, representing 26 failures in single-record/single-failure data 306 total analysis time at risk and under observation at risk from t = 0 earliest observed entry t = 0 last observed exit t = 6 . sts list //Kaplan-Meier failure _d: folstatus == 1 analysis time _t: catyrfol Beg. Net Survivor Std. Time Total Fail Lost Function Error [95% Conf. Int.] ------------------------------------------------------------------------------- 2 75 11 0 0.8533 0.0409 0.7508 0.9160 4 64 11 39 0.7067 0.0526 0.5895 0.7960 6 14 4 10 0.5048 0.0932 0.3132 0.6686 ------------------------------------------------------------------------------- . sts list, cumhaz //Cumulative Hazard failure _d: folstatus == 1 analysis time _t: catyrfol Beg. Net Nelson-Aalen Std. Time Total Fail Lost Cum. Haz. Error [95% Conf. Int.] ------------------------------------------------------------------------------- 2 75 11 0 0.1467 0.0442 0.0812 0.2648 4 64 11 39 0.3185 0.0681 0.2095 0.4844 6 14 4 10 0.6043 0.1583 0.3616 1.0097 -------------------------------------------------------------------------------
\[ \hat{S}(t)\,=\,\prod_{(j|t_{j}\leq t)} \left(\frac{n_{j}\,-\,d_{j}}{n_{j}}\right) \]
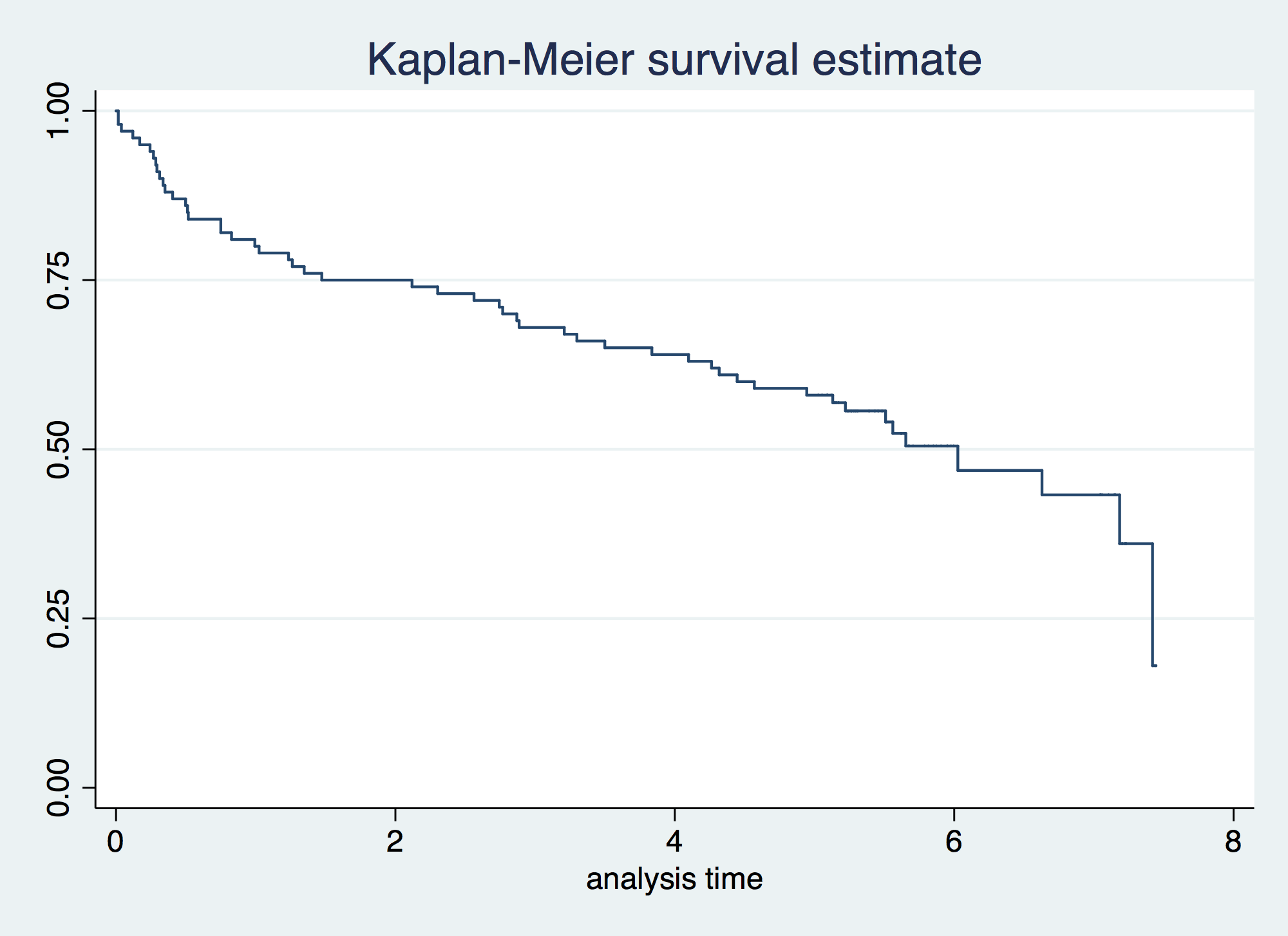
. qui: stset foltime, fail(folstatus==1) scale(365.25) // Using the computed time . . sts graph failure _d: folstatus == 1 analysis time _t: foltime/365.25

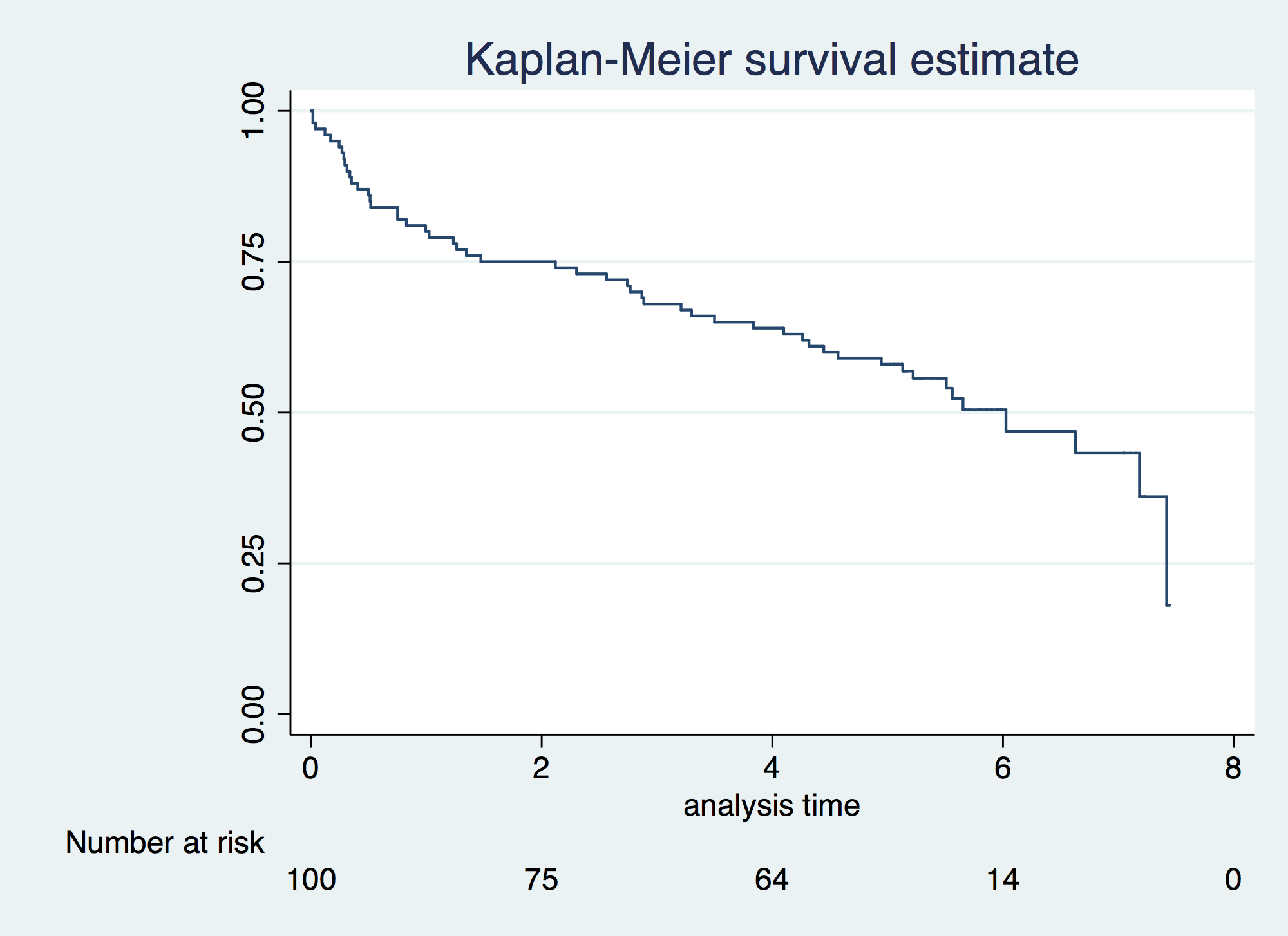
. sts generate svar = s . . sts graph, risktable failure _d: folstatus == 1 analysis time _t: foltime/365.25
. sts graph, by(gender) risktable failure _d: folstatus == 1 analysis time _t: foltime/365.25
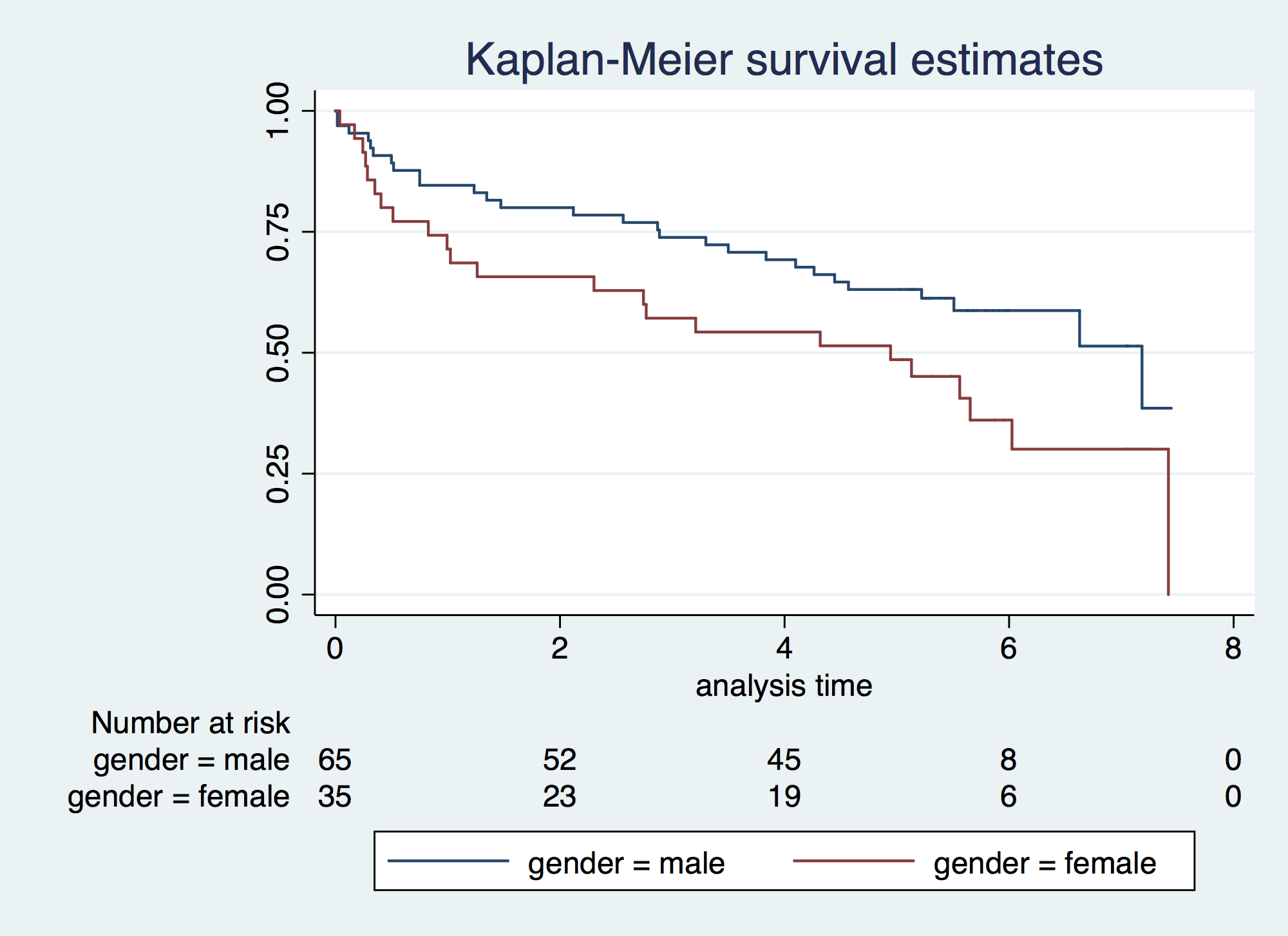
. stci failure _d: folstatus == 1 analysis time _t: foltime/365.25 | no. of | subjects 50% Std. Err. [95% Conf. Interval] -------------+------------------------------------------------------------- total | 100 6.02601 .5603603 4.44627 7.41958 . stci, p(25) failure _d: folstatus == 1 analysis time _t: foltime/365.25 | no. of | subjects 25% Std. Err. [95% Conf. Interval] -------------+------------------------------------------------------------- total | 100 1.472964 .7682197 .750171 3.29911
. stsum //Overall Incidence Rate and PTR (use it for your abstract and the results section of > your paper) failure _d: folstatus == 1 analysis time _t: foltime/365.25 | incidence no. of |------ Survival time -----| | time at risk rate subjects 25% 50% 75% ---------+--------------------------------------------------------------------- total | 412.1560575 .1237395 100 1.472964 6.02601 7.419576 . stsum, by(gender) //By levels of your categorical variables. Note 95%CI is not provided > failure _d: folstatus == 1 analysis time _t: foltime/365.25 | incidence no. of |------ Survival time -----| gender | time at risk rate subjects 25% 50% 75% ---------+--------------------------------------------------------------------- male | 284.2299795 .0985118 65 2.885695 7.18412 . female | 127.926078 .1797913 35 .8268309 4.944559 7.419576 ---------+--------------------------------------------------------------------- total | 412.1560575 .1237395 100 1.472964 6.02601 7.419576
\[ H(t)\,=\,\sum_{(j|t_{j}\leq t)}\frac{d_{j}}{n_{j}} \]
. sts graph, cumhaz failure _d: folstatus == 1 analysis time _t: foltime/365.25
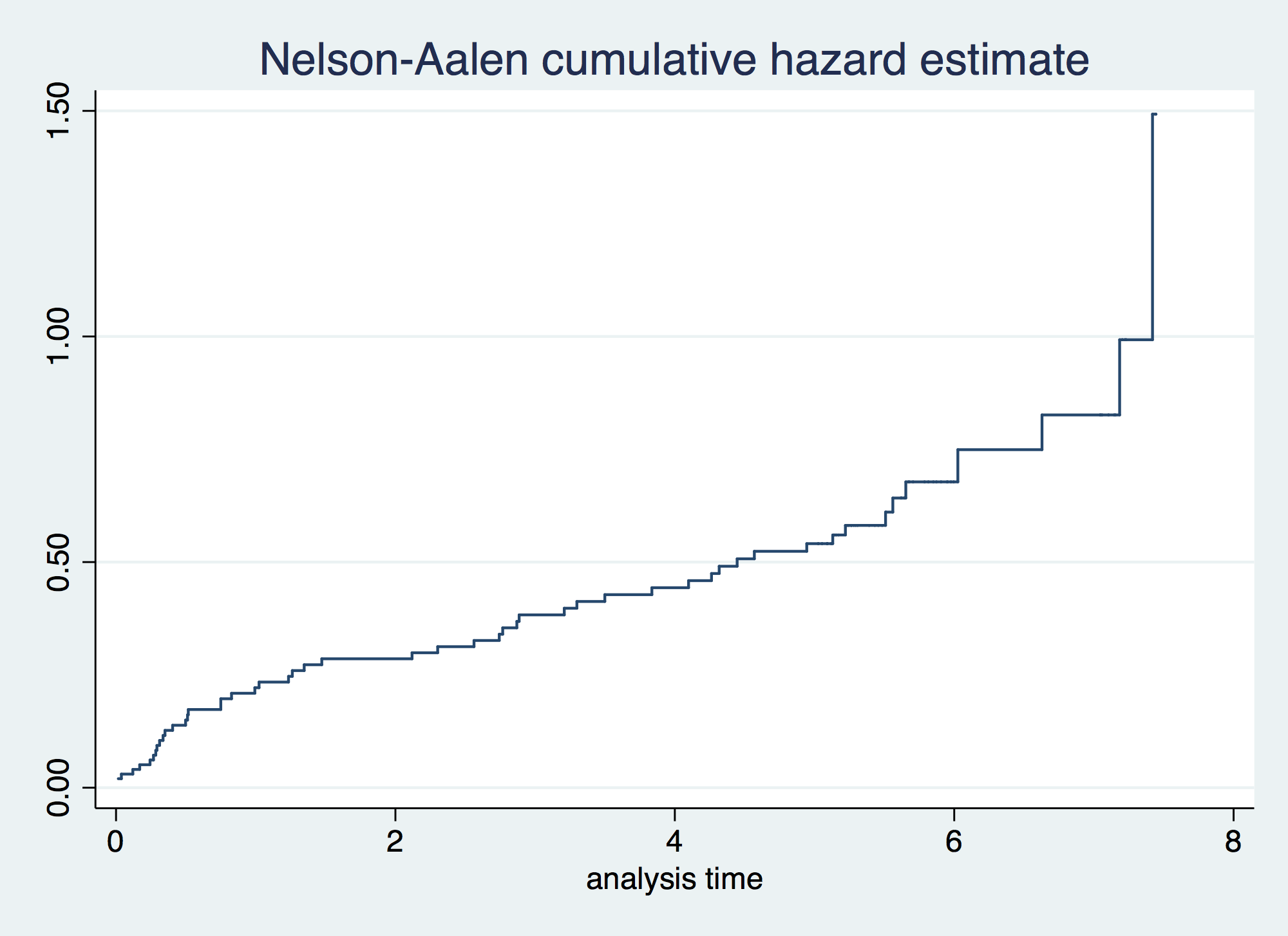
. sts graph, cumhaz by(gender) failure _d: folstatus == 1 analysis time _t: foltime/365.25
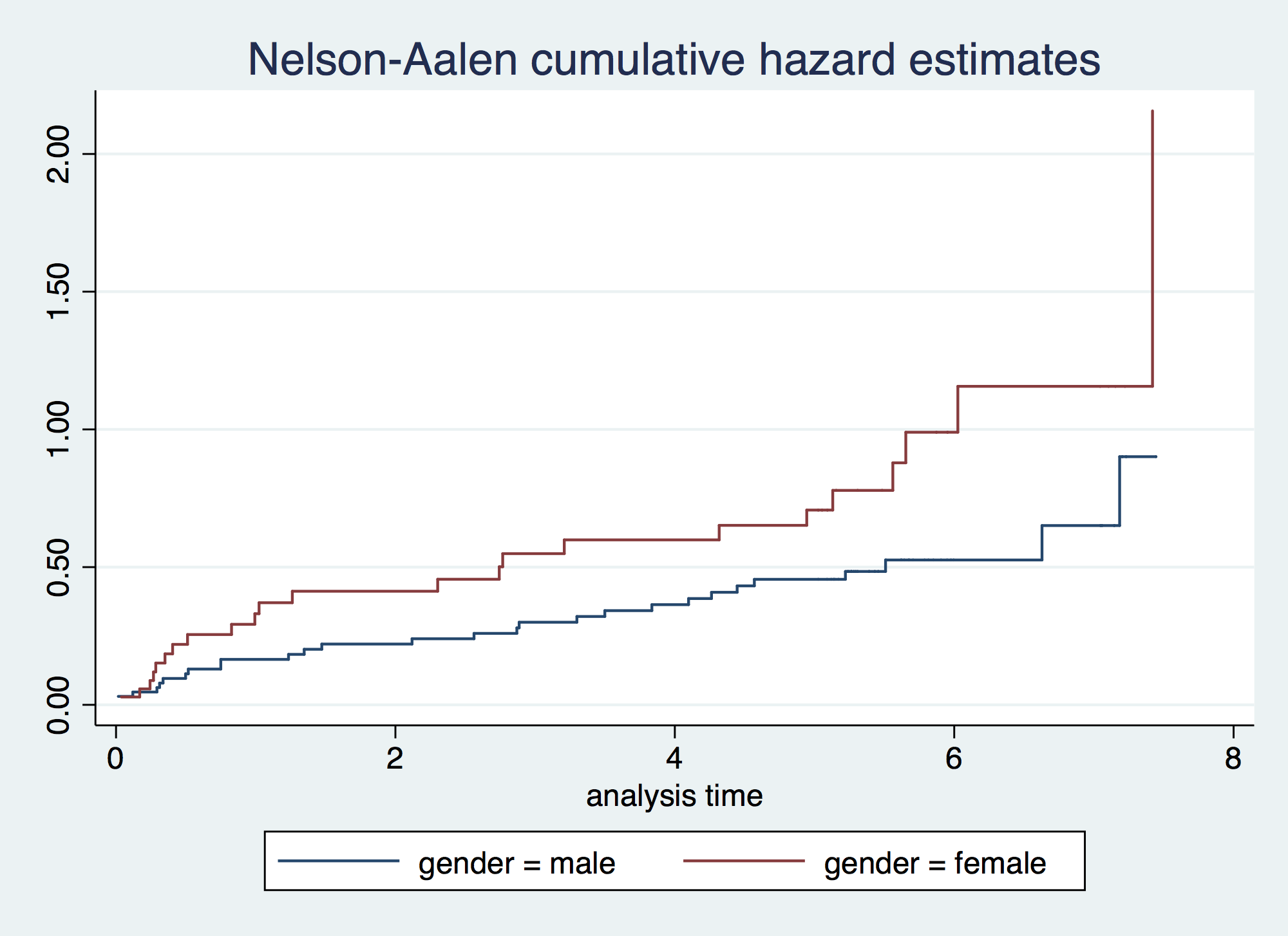
. sum yrfol // Y = Mean followup x N = Years at risk Variable | Obs Mean Std. Dev. Min Max -------------+--------------------------------------------------------- yrfol | 100 4.121561 2.351538 .0164271 7.444216 . strate // Y = 412.2 years at risk and Incidence Density or Rate per person-year at risk failure _d: folstatus == 1 analysis time _t: foltime/365.25 Estimated rates and lower/upper bounds of 95% confidence intervals (100 records included in the analysis) +------------------------------------------------+ | D Y Rate Lower Upper | |------------------------------------------------| | 51 412.1561 0.123740 0.094041 0.162817 | +------------------------------------------------+ . . gen n = 1 . tabrate folstatus gender, exp(n) per(1000) // Cumulative incidence (Proportion) over 8 years table of cases (D), person-years (Y), and rates per 1000 person-years +--------------------------------------------------+ | gender _D _Y _rate ci_low ci_high | |--------------------------------------------------| | male 28 65.0 430.769 297.429 623.888 | | female 23 35.0 657.143 436.689 988.889 | +--------------------------------------------------+ Chisq test for unequal rates = 2.29 (1 df, p = 0.131 ) . . strate gender, per(1000) // Incidence Density or Rate per 1000 person-year at risk failure _d: folstatus == 1 analysis time _t: foltime/365.25 Estimated rates (per 1000) and lower/upper bounds of 95% confidence intervals (100 records included in the analysis) +----------------------------------------------------+ | gender D Y Rate Lower Upper | |----------------------------------------------------| | male 28 0.2842 98.512 68.018 142.676 | | female 23 0.1279 179.791 119.476 270.556 | +----------------------------------------------------+ . stmh gender, c(1,0) failure _d: folstatus == 1 analysis time _t: foltime/365.25 Maximum likelihood estimate of the rate ratio comparing gender==1 vs. gender==0 RR estimate, and lower and upper 95% confidence limits ---------------------------------------------------------- RR chi2 P>chi2 [95% Conf. Interval] ---------------------------------------------------------- 1.825 4.71 0.0300 1.051 3.168 ----------------------------------------------------------
. stmh gender, by(age) c(1,0) failure _d: folstatus == 1 analysis time _t: foltime/365.25 Maximum likelihood estimate of the rate ratio comparing gender==1 vs. gender==0 by age RR estimate, and lower and upper 95% confidence limits +----------------------------+ | age RR Lower Upper | |----------------------------| | 43 . . . | | 48 0.00 . . | | 60 0.00 . . | | 64 . . . | | 66 1.67 0.10 26.63 | |----------------------------| | 72 0.00 . . | | 73 0.49 0.03 7.86 | | 76 1.04 0.06 16.57 | | 77 0.00 . . | | 80 0.00 . . | |----------------------------| | 81 . . . | | 82 1.23 0.11 13.52 | | 83 1.02 0.09 11.28 | | 85 0.08 0.01 0.88 | | 86 4.42 0.28 70.65 | +----------------------------+ Overall estimate controlling for age ---------------------------------------------------------- RR chi2 P>chi2 [95% Conf. Interval] ---------------------------------------------------------- 1.009 0.00 0.9765 0.543 1.877 ---------------------------------------------------------- Approx test for unequal RRs (effect modification): chi2(14) = 65.21 Pr>chi2 = 0.0000
\[ H(t)\,=\,-\text{ln}\left[\text(S(t))\right] \]
\[ S(t)\,=\,\text{exp}\left[\text(-H(t))\right] \]
. sts generate kmS = s // Obtain KM survivor estimate . sts generate naH = na // Obtain NA cum. hazard estimate . gen naS = exp(-naH) // Calculate NA survivor estimate . gen kmH = -log(kmS) // Calculate KM cum. harzard estimate . label var kmS "KM" . label var naS "exp(-NA)" . label var kmH "-log(KM)" . label var naH "NA" . twoway connected kmS naS _t, connect(J J) sort // Survivor estimate using NA always > than K > M (simulations)
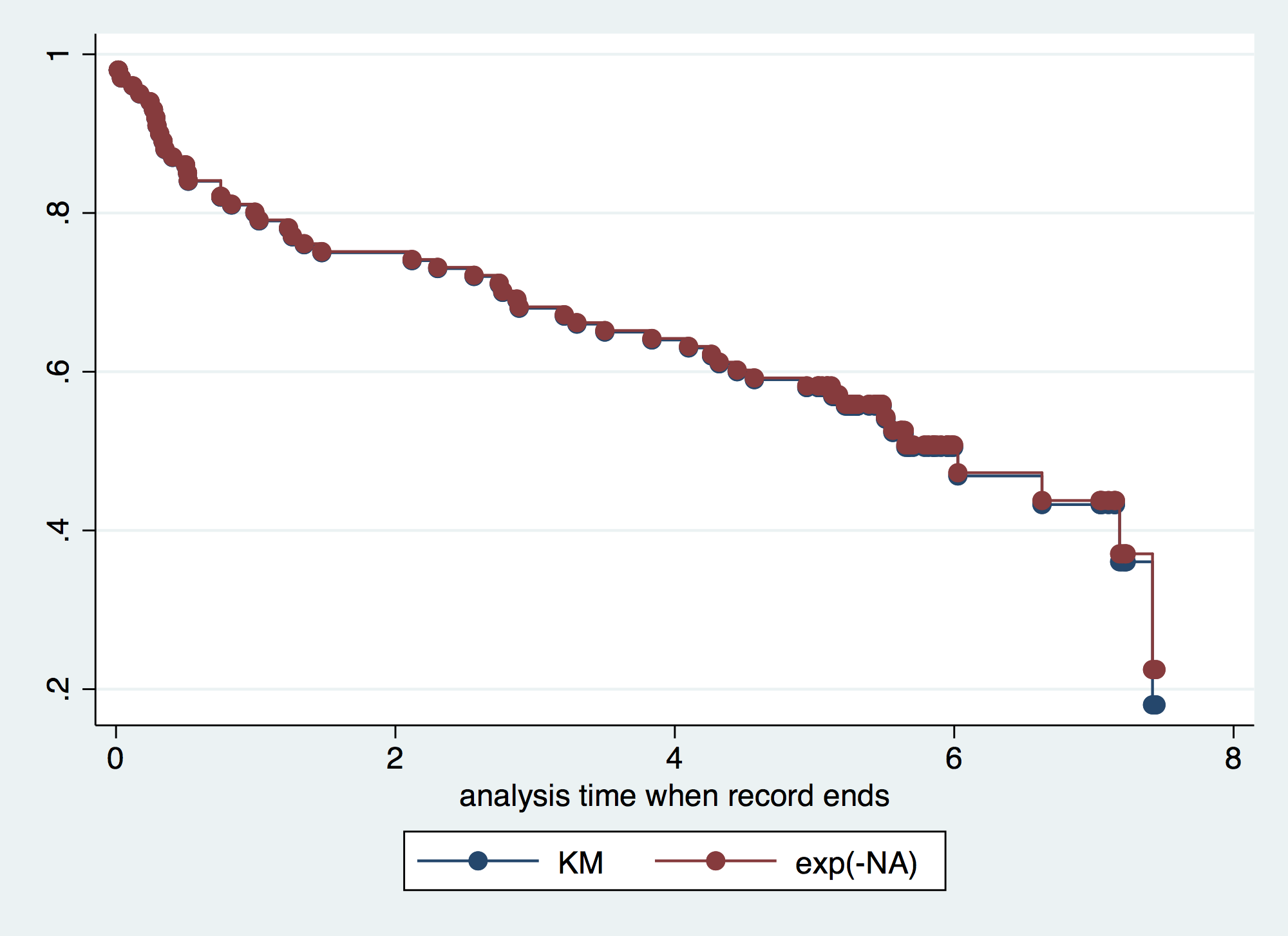
. twoway connected kmH naH _t, connect(J J) sort
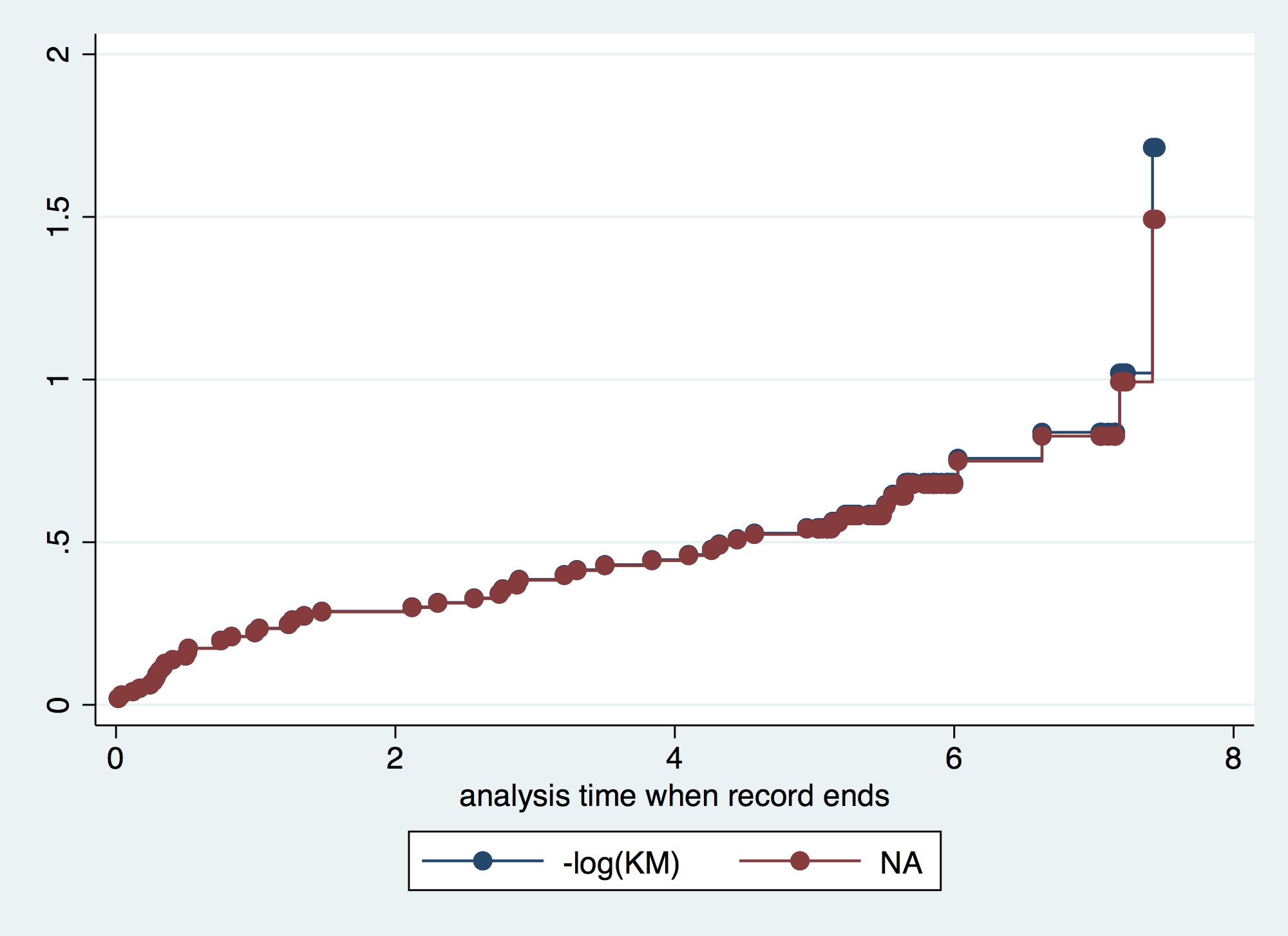
. sts list, by(gender) compare // Survival failure _d: folstatus == 1 analysis time _t: foltime/365.25 Survivor Function gender male female ---------------------------------- time 0 1.0000 1.0000 .928474 0.8462 0.7429 1.85695 0.8000 0.6571 2.78542 0.7692 0.5714 3.71389 0.7077 0.5429 4.64237 0.6308 0.5143 5.57084 0.5872 0.4059 6.49932 0.5872 0.3007 7.42779 0.3854 . 8.35626 . . ---------------------------------- . sts list, na by(gender) compare // Cumulative Hazard failure _d: folstatus == 1 analysis time _t: foltime/365.25 Nelson-Aalen Cum. Haz. gender male female ---------------------------------- time 0 0.0000 0.0000 .928474 0.1651 0.2924 1.85695 0.2207 0.4125 2.78542 0.2595 0.5490 3.71389 0.3420 0.5990 4.64237 0.4558 0.6517 5.57084 0.5260 0.8787 6.49932 0.5260 1.1564 7.42779 0.9010 . 8.35626 . . ---------------------------------- . sts test gender, logrank // Logrank Test (it is an extension of the Mantel-Haenszel applied > to survival) failure _d: folstatus == 1 analysis time _t: foltime/365.25 Log-rank test for equality of survivor functions | Events Events gender | observed expected -------+------------------------- male | 28 34.62 female | 23 16.38 -------+------------------------- Total | 51 51.00 chi2(1) = 3.97 Pr>chi2 = 0.0463
. sum age Variable | Obs Mean Std. Dev. Min Max -------------+--------------------------------------------------------- age | 100 68.25 14.42807 32 92 . egen agecat = cut(age), at(30,50,80,100) . sts graph, by(agecat) risktable gwood failure _d: folstatus == 1 analysis time _t: foltime/365.25
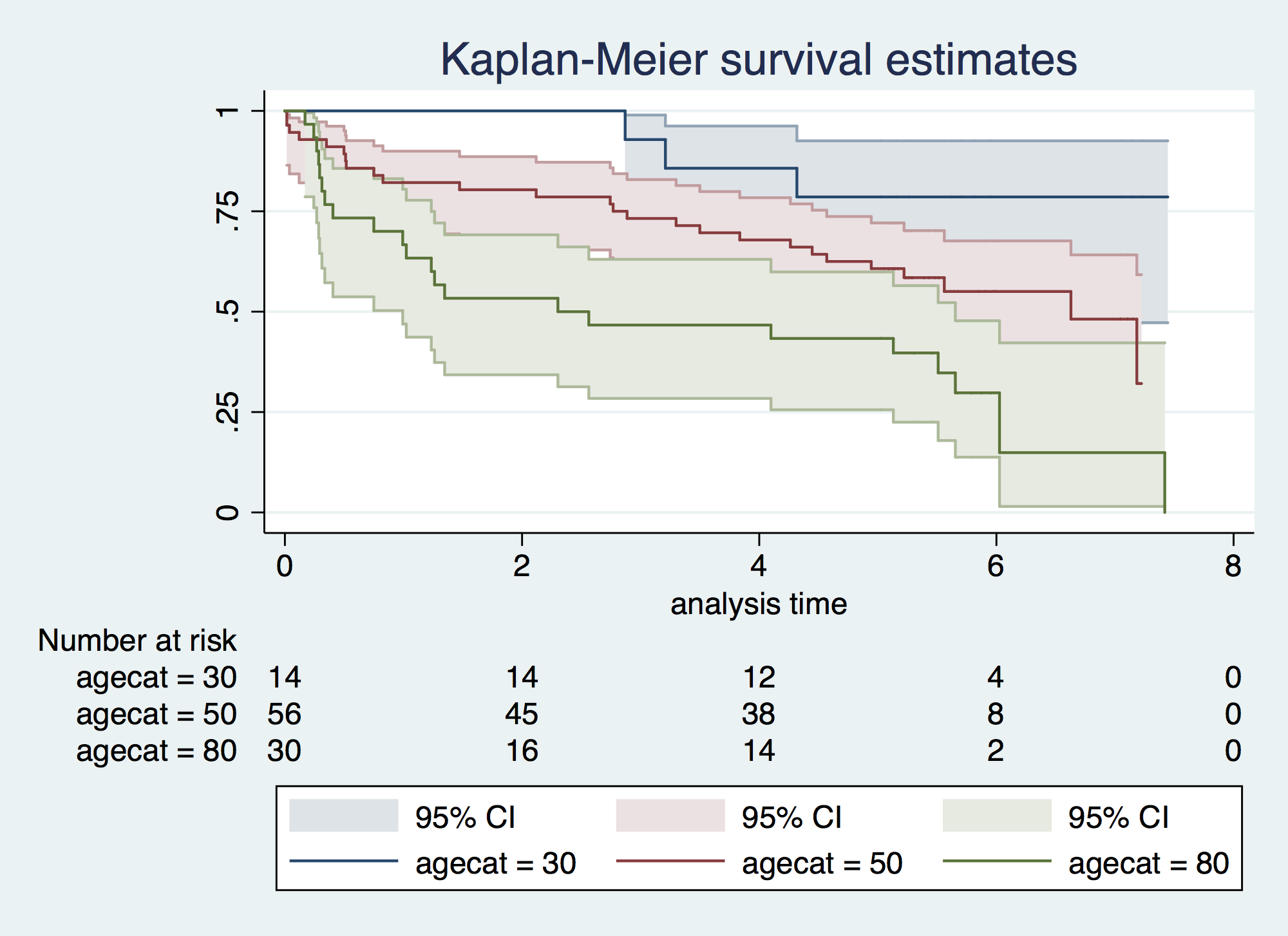
. sts test agecat, trend logrank failure _d: folstatus == 1 analysis time _t: foltime/365.25 Log-rank test for equality of survivor functions | Events Events agecat | observed expected -------+------------------------- 30 | 3 9.75 50 | 26 28.91 80 | 22 12.34 -------+------------------------- Total | 51 51.00 chi2(2) = 12.73 Pr>chi2 = 0.0017 Test for trend of survivor functions chi2(1) = 12.73 Pr>chi2 = 0.0004
. sts list // very small number of ties failure _d: folstatus == 1 analysis time _t: foltime/365.25 Beg. Net Survivor Std. Time Total Fail Lost Function Error [95% Conf. Int.] ------------------------------------------------------------------------------- .0164 100 2 0 0.9800 0.0140 0.9224 0.9950 .0383 98 1 0 0.9700 0.0171 0.9099 0.9902 .1205 97 1 0 0.9600 0.0196 0.8969 0.9848 .1697 96 1 0 0.9500 0.0218 0.8840 0.9789 .2437 95 1 0 0.9400 0.0237 0.8713 0.9726 .2683 94 1 0 0.9300 0.0255 0.8588 0.9660 .2847 93 1 0 0.9200 0.0271 0.8464 0.9592 .293 92 1 0 0.9100 0.0286 0.8342 0.9521 .3121 91 1 0 0.9000 0.0300 0.8221 0.9449 .3368 90 1 0 0.8900 0.0313 0.8102 0.9375 .3504 89 1 0 0.8800 0.0325 0.7984 0.9300 .4052 88 1 0 0.8700 0.0336 0.7867 0.9224 .4983 87 1 0 0.8600 0.0347 0.7751 0.9146 .512 86 1 0 0.8500 0.0357 0.7636 0.9067 .5175 85 1 0 0.8400 0.0367 0.7522 0.8988 .7502 84 2 0 0.8200 0.0384 0.7296 0.8826 .8268 82 1 0 0.8100 0.0392 0.7185 0.8743 .9938 81 1 0 0.8000 0.0400 0.7074 0.8660 1.024 80 1 0 0.7900 0.0407 0.6964 0.8577 1.235 79 1 0 0.7800 0.0414 0.6854 0.8492 1.262 78 1 0 0.7700 0.0421 0.6745 0.8407 1.347 77 1 0 0.7600 0.0427 0.6637 0.8322 1.473 76 1 0 0.7500 0.0433 0.6529 0.8236 2.119 75 1 0 0.7400 0.0439 0.6422 0.8149 2.303 74 1 0 0.7300 0.0444 0.6315 0.8061 2.563 73 1 0 0.7200 0.0449 0.6209 0.7974 2.743 72 1 0 0.7100 0.0454 0.6103 0.7885 2.768 71 1 0 0.7000 0.0458 0.5998 0.7797 2.869 70 1 0 0.6900 0.0462 0.5894 0.7707 2.886 69 1 0 0.6800 0.0466 0.5790 0.7617 3.209 68 1 0 0.6700 0.0470 0.5686 0.7527 3.299 67 1 0 0.6600 0.0474 0.5583 0.7437 3.499 66 1 0 0.6500 0.0477 0.5480 0.7345 3.836 65 1 0 0.6400 0.0480 0.5377 0.7254 4.099 64 1 0 0.6300 0.0483 0.5275 0.7162 4.263 63 1 0 0.6200 0.0485 0.5174 0.7070 4.318 62 1 0 0.6100 0.0488 0.5073 0.6977 4.446 61 1 0 0.6000 0.0490 0.4972 0.6884 4.569 60 1 0 0.5900 0.0492 0.4872 0.6790 4.945 59 1 0 0.5800 0.0494 0.4772 0.6696 5.027 58 0 2 0.5800 0.0494 0.4772 0.6696 5.054 56 0 1 0.5800 0.0494 0.4772 0.6696 5.09 55 0 1 0.5800 0.0494 0.4772 0.6696 5.092 54 0 1 0.5800 0.0494 0.4772 0.6696 5.12 53 0 1 0.5800 0.0494 0.4772 0.6696 5.131 52 1 0 0.5688 0.0497 0.4658 0.6593 5.136 51 0 1 0.5688 0.0497 0.4658 0.6593 5.144 50 0 1 0.5688 0.0497 0.4658 0.6593 5.155 49 0 1 0.5688 0.0497 0.4658 0.6593 5.172 48 0 1 0.5688 0.0497 0.4658 0.6593 5.221 47 1 0 0.5567 0.0500 0.4533 0.6482 5.235 46 0 1 0.5567 0.0500 0.4533 0.6482 5.246 45 0 1 0.5567 0.0500 0.4533 0.6482 5.262 44 0 1 0.5567 0.0500 0.4533 0.6482 5.265 43 0 1 0.5567 0.0500 0.4533 0.6482 5.281 42 0 1 0.5567 0.0500 0.4533 0.6482 5.295 41 0 1 0.5567 0.0500 0.4533 0.6482 5.309 40 0 2 0.5567 0.0500 0.4533 0.6482 5.391 38 0 1 0.5567 0.0500 0.4533 0.6482 5.432 37 0 1 0.5567 0.0500 0.4533 0.6482 5.457 36 0 1 0.5567 0.0500 0.4533 0.6482 5.484 35 0 1 0.5567 0.0500 0.4533 0.6482 5.509 34 1 0 0.5404 0.0512 0.4351 0.6343 5.511 33 0 1 0.5404 0.0512 0.4351 0.6343 5.561 32 1 0 0.5235 0.0523 0.4165 0.6198 5.618 31 0 1 0.5235 0.0523 0.4165 0.6198 5.624 30 0 1 0.5235 0.0523 0.4165 0.6198 5.643 29 0 1 0.5235 0.0523 0.4165 0.6198 5.654 28 1 0 0.5048 0.0537 0.3956 0.6041 5.673 27 0 1 0.5048 0.0537 0.3956 0.6041 5.678 26 0 1 0.5048 0.0537 0.3956 0.6041 5.706 25 0 1 0.5048 0.0537 0.3956 0.6041 5.788 24 0 1 0.5048 0.0537 0.3956 0.6041 5.815 23 0 1 0.5048 0.0537 0.3956 0.6041 5.851 22 0 2 0.5048 0.0537 0.3956 0.6041 5.873 20 0 1 0.5048 0.0537 0.3956 0.6041 5.906 19 0 1 0.5048 0.0537 0.3956 0.6041 5.949 18 0 1 0.5048 0.0537 0.3956 0.6041 5.952 17 0 1 0.5048 0.0537 0.3956 0.6041 5.977 16 0 1 0.5048 0.0537 0.3956 0.6041 5.996 15 0 1 0.5048 0.0537 0.3956 0.6041 6.026 14 1 0 0.4687 0.0607 0.3466 0.5816 6.628 13 1 0 0.4327 0.0659 0.3023 0.5562 7.044 12 0 1 0.4327 0.0659 0.3023 0.5562 7.047 11 0 1 0.4327 0.0659 0.3023 0.5562 7.058 10 0 1 0.4327 0.0659 0.3023 0.5562 7.105 9 0 1 0.4327 0.0659 0.3023 0.5562 7.146 8 0 1 0.4327 0.0659 0.3023 0.5562 7.154 7 0 1 0.4327 0.0659 0.3023 0.5562 7.184 6 1 0 0.3606 0.0857 0.1997 0.5241 7.203 5 0 1 0.3606 0.0857 0.1997 0.5241 7.222 4 0 1 0.3606 0.0857 0.1997 0.5241 7.231 3 0 1 0.3606 0.0857 0.1997 0.5241 7.42 2 1 0 0.1803 0.1345 0.0179 0.4820 7.444 1 0 1 0.1803 0.1345 0.0179 0.4820 ------------------------------------------------------------------------------- . stcox gender // Breslow estimate for ties failure _d: folstatus == 1 analysis time _t: foltime/365.25 Iteration 0: log likelihood = -209.11972 Iteration 1: log likelihood = -207.2544 Iteration 2: log likelihood = -207.2423 Iteration 3: log likelihood = -207.2423 Refining estimates: Iteration 0: log likelihood = -207.2423 Cox regression -- Breslow method for ties No. of subjects = 100 Number of obs = 100 No. of failures = 51 Time at risk = 412.1560575 LR chi2(1) = 3.75 Log likelihood = -207.2423 Prob > chi2 = 0.0527 ------------------------------------------------------------------------------ _t | Haz. Ratio Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- gender | 1.742761 .4921308 1.97 0.049 1.002006 3.031133 ------------------------------------------------------------------------------ . stcox gender, efron // Mor accurate than Breslow failure _d: folstatus == 1 analysis time _t: foltime/365.25 Iteration 0: log likelihood = -209.09769 Iteration 1: log likelihood = -207.23669 Iteration 2: log likelihood = -207.22467 Iteration 3: log likelihood = -207.22467 Refining estimates: Iteration 0: log likelihood = -207.22467 Cox regression -- Efron method for ties No. of subjects = 100 Number of obs = 100 No. of failures = 51 Time at risk = 412.1560575 LR chi2(1) = 3.75 Log likelihood = -207.22467 Prob > chi2 = 0.0529 ------------------------------------------------------------------------------ _t | Haz. Ratio Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- gender | 1.741613 .4918126 1.96 0.049 1.00134 3.029157 ------------------------------------------------------------------------------ . . . stcox i.gender // Indicator variables failure _d: folstatus == 1 analysis time _t: foltime/365.25 Iteration 0: log likelihood = -209.11972 Iteration 1: log likelihood = -207.2544 Iteration 2: log likelihood = -207.2423 Iteration 3: log likelihood = -207.2423 Refining estimates: Iteration 0: log likelihood = -207.2423 Cox regression -- Breslow method for ties No. of subjects = 100 Number of obs = 100 No. of failures = 51 Time at risk = 412.1560575 LR chi2(1) = 3.75 Log likelihood = -207.2423 Prob > chi2 = 0.0527 ------------------------------------------------------------------------------ _t | Haz. Ratio Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- gender | female | 1.742761 .4921308 1.97 0.049 1.002006 3.031133 ------------------------------------------------------------------------------ . . tab agecat agecat | Freq. Percent Cum. ------------+----------------------------------- 30 | 14 14.00 14.00 50 | 56 56.00 70.00 80 | 30 30.00 100.00 ------------+----------------------------------- Total | 100 100.00 . stcox i.agecat // Categorical variables (Contrast indicator and wald test) failure _d: folstatus == 1 analysis time _t: foltime/365.25 Iteration 0: log likelihood = -209.11972 Iteration 1: log likelihood = -203.05446 Iteration 2: log likelihood = -202.59595 Iteration 3: log likelihood = -202.59206 Iteration 4: log likelihood = -202.59206 Refining estimates: Iteration 0: log likelihood = -202.59206 Cox regression -- Breslow method for ties No. of subjects = 100 Number of obs = 100 No. of failures = 51 Time at risk = 412.1560575 LR chi2(2) = 13.06 Log likelihood = -202.59206 Prob > chi2 = 0.0015 ------------------------------------------------------------------------------ _t | Haz. Ratio Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- agecat | 50 | 2.950289 1.807422 1.77 0.077 .8879672 9.802395 80 | 5.934847 3.668544 2.88 0.004 1.767059 19.93279 ------------------------------------------------------------------------------ . . stcox age // Continuous variables interpretation and scale failure _d: folstatus == 1 analysis time _t: foltime/365.25 Iteration 0: log likelihood = -209.11972 Iteration 1: log likelihood = -200.64424 Iteration 2: log likelihood = -200.44425 Iteration 3: log likelihood = -200.44391 Refining estimates: Iteration 0: log likelihood = -200.44391 Cox regression -- Breslow method for ties No. of subjects = 100 Number of obs = 100 No. of failures = 51 Time at risk = 412.1560575 LR chi2(1) = 17.35 Log likelihood = -200.44391 Prob > chi2 = 0.0000 ------------------------------------------------------------------------------ _t | Haz. Ratio Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- age | 1.04672 .0125089 3.82 0.000 1.022488 1.071527 ------------------------------------------------------------------------------ . gen age5 = age/5 . stcox age5 failure _d: folstatus == 1 analysis time _t: foltime/365.25 Iteration 0: log likelihood = -209.11972 Iteration 1: log likelihood = -200.64424 Iteration 2: log likelihood = -200.44425 Iteration 3: log likelihood = -200.44391 Refining estimates: Iteration 0: log likelihood = -200.44391 Cox regression -- Breslow method for ties No. of subjects = 100 Number of obs = 100 No. of failures = 51 Time at risk = 412.1560575 LR chi2(1) = 17.35 Log likelihood = -200.44391 Prob > chi2 = 0.0000 ------------------------------------------------------------------------------ _t | Haz. Ratio Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- age5 | 1.256473 .0750778 3.82 0.000 1.117613 1.412586 ------------------------------------------------------------------------------ . . stcox c.age##c.age // Functional form age: No evidence of nonlinear effect (quadratic) failure _d: folstatus == 1 analysis time _t: foltime/365.25 Iteration 0: log likelihood = -209.11972 Iteration 1: log likelihood = -200.17407 Iteration 2: log likelihood = -199.58078 Iteration 3: log likelihood = -199.57967 Iteration 4: log likelihood = -199.57967 Refining estimates: Iteration 0: log likelihood = -199.57967 Cox regression -- Breslow method for ties No. of subjects = 100 Number of obs = 100 No. of failures = 51 Time at risk = 412.1560575 LR chi2(2) = 19.08 Log likelihood = -199.57967 Prob > chi2 = 0.0001 ------------------------------------------------------------------------------ _t | Haz. Ratio Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- age | .9222841 .0850547 -0.88 0.380 .7697777 1.105005 | c.age#c.age | 1.000944 .000689 1.37 0.170 .9995945 1.002295 ------------------------------------------------------------------------------ . . stcox i.gender##c.age // Interactions: small evidence effect modification of age failure _d: folstatus == 1 analysis time _t: foltime/365.25 Iteration 0: log likelihood = -209.11972 Iteration 1: log likelihood = -199.57097 Iteration 2: log likelihood = -198.9633 Iteration 3: log likelihood = -198.95656 Iteration 4: log likelihood = -198.95655 Refining estimates: Iteration 0: log likelihood = -198.95655 Cox regression -- Breslow method for ties No. of subjects = 100 Number of obs = 100 No. of failures = 51 Time at risk = 412.1560575 LR chi2(3) = 20.33 Log likelihood = -198.95655 Prob > chi2 = 0.0001 ------------------------------------------------------------------------------ _t | Haz. Ratio Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- gender | female | 25.7504 47.048 1.78 0.075 .717088 924.6889 age | 1.06086 .0171645 3.65 0.000 1.027746 1.095041 | gender#c.age | female | .959227 .0234825 -1.70 0.089 .9142888 1.006374 ------------------------------------------------------------------------------ . . stcox i.gender age // Age as confounder. Note: consider the interpretation of gender failure _d: folstatus == 1 analysis time _t: foltime/365.25 Iteration 0: log likelihood = -209.11972 Iteration 1: log likelihood = -200.5215 Iteration 2: log likelihood = -200.3233 Iteration 3: log likelihood = -200.323 Refining estimates: Iteration 0: log likelihood = -200.323 Cox regression -- Breslow method for ties No. of subjects = 100 Number of obs = 100 No. of failures = 51 Time at risk = 412.1560575 LR chi2(2) = 17.59 Log likelihood = -200.323 Prob > chi2 = 0.0002 ------------------------------------------------------------------------------ _t | Haz. Ratio Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- gender | female | 1.16075 .351101 0.49 0.622 .6416069 2.099946 age | 1.044538 .0132085 3.45 0.001 1.018968 1.07075 ------------------------------------------------------------------------------ . . gen age30 = age - 30 . stcox i.gender age30 // More meaninful interpretation (mean centering age) failure _d: folstatus == 1 analysis time _t: foltime/365.25 Iteration 0: log likelihood = -209.11972 Iteration 1: log likelihood = -200.5215 Iteration 2: log likelihood = -200.3233 Iteration 3: log likelihood = -200.323 Refining estimates: Iteration 0: log likelihood = -200.323 Cox regression -- Breslow method for ties No. of subjects = 100 Number of obs = 100 No. of failures = 51 Time at risk = 412.1560575 LR chi2(2) = 17.59 Log likelihood = -200.323 Prob > chi2 = 0.0002 ------------------------------------------------------------------------------ _t | Haz. Ratio Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- gender | female | 1.16075 .351101 0.49 0.622 .6416069 2.099946 age30 | 1.044538 .0132085 3.45 0.001 1.018968 1.07075 ------------------------------------------------------------------------------ . . stcox gender // Likelihood Ratio Test failure _d: folstatus == 1 analysis time _t: foltime/365.25 Iteration 0: log likelihood = -209.11972 Iteration 1: log likelihood = -207.2544 Iteration 2: log likelihood = -207.2423 Iteration 3: log likelihood = -207.2423 Refining estimates: Iteration 0: log likelihood = -207.2423 Cox regression -- Breslow method for ties No. of subjects = 100 Number of obs = 100 No. of failures = 51 Time at risk = 412.1560575 LR chi2(1) = 3.75 Log likelihood = -207.2423 Prob > chi2 = 0.0527 ------------------------------------------------------------------------------ _t | Haz. Ratio Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- gender | 1.742761 .4921308 1.97 0.049 1.002006 3.031133 ------------------------------------------------------------------------------ . estimates store A . stcox gender age failure _d: folstatus == 1 analysis time _t: foltime/365.25 Iteration 0: log likelihood = -209.11972 Iteration 1: log likelihood = -200.5215 Iteration 2: log likelihood = -200.3233 Iteration 3: log likelihood = -200.323 Refining estimates: Iteration 0: log likelihood = -200.323 Cox regression -- Breslow method for ties No. of subjects = 100 Number of obs = 100 No. of failures = 51 Time at risk = 412.1560575 LR chi2(2) = 17.59 Log likelihood = -200.323 Prob > chi2 = 0.0002 ------------------------------------------------------------------------------ _t | Haz. Ratio Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- gender | 1.16075 .351101 0.49 0.622 .6416069 2.099946 age | 1.044538 .0132085 3.45 0.001 1.018968 1.07075 ------------------------------------------------------------------------------ . estimates store B . lrtest A B Likelihood-ratio test LR chi2(1) = 13.84 (Assumption: A nested in B) Prob > chi2 = 0.0002 . . tab agecat gender, row chi // Do not forget crosstabulations: understanding your data is KEY > ! +----------------+ | Key | |----------------| | frequency | | row percentage | +----------------+ | gender agecat | male female | Total -----------+----------------------+---------- 30 | 11 3 | 14 | 78.57 21.43 | 100.00 -----------+----------------------+---------- 50 | 41 15 | 56 | 73.21 26.79 | 100.00 -----------+----------------------+---------- 80 | 13 17 | 30 | 43.33 56.67 | 100.00 -----------+----------------------+---------- Total | 65 35 | 100 | 65.00 35.00 | 100.00 Pearson chi2(2) = 8.9848 Pr = 0.011
. stcox gender age30 failure _d: folstatus == 1 analysis time _t: foltime/365.25 Iteration 0: log likelihood = -209.11972 Iteration 1: log likelihood = -200.5215 Iteration 2: log likelihood = -200.3233 Iteration 3: log likelihood = -200.323 Refining estimates: Iteration 0: log likelihood = -200.323 Cox regression -- Breslow method for ties No. of subjects = 100 Number of obs = 100 No. of failures = 51 Time at risk = 412.1560575 LR chi2(2) = 17.59 Log likelihood = -200.323 Prob > chi2 = 0.0002 ------------------------------------------------------------------------------ _t | Haz. Ratio Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- gender | 1.16075 .351101 0.49 0.622 .6416069 2.099946 age30 | 1.044538 .0132085 3.45 0.001 1.018968 1.07075 ------------------------------------------------------------------------------ . . predict H0, basechazard // Baseline cumulative hazard function . tw line H0 _t, connect (J) sort
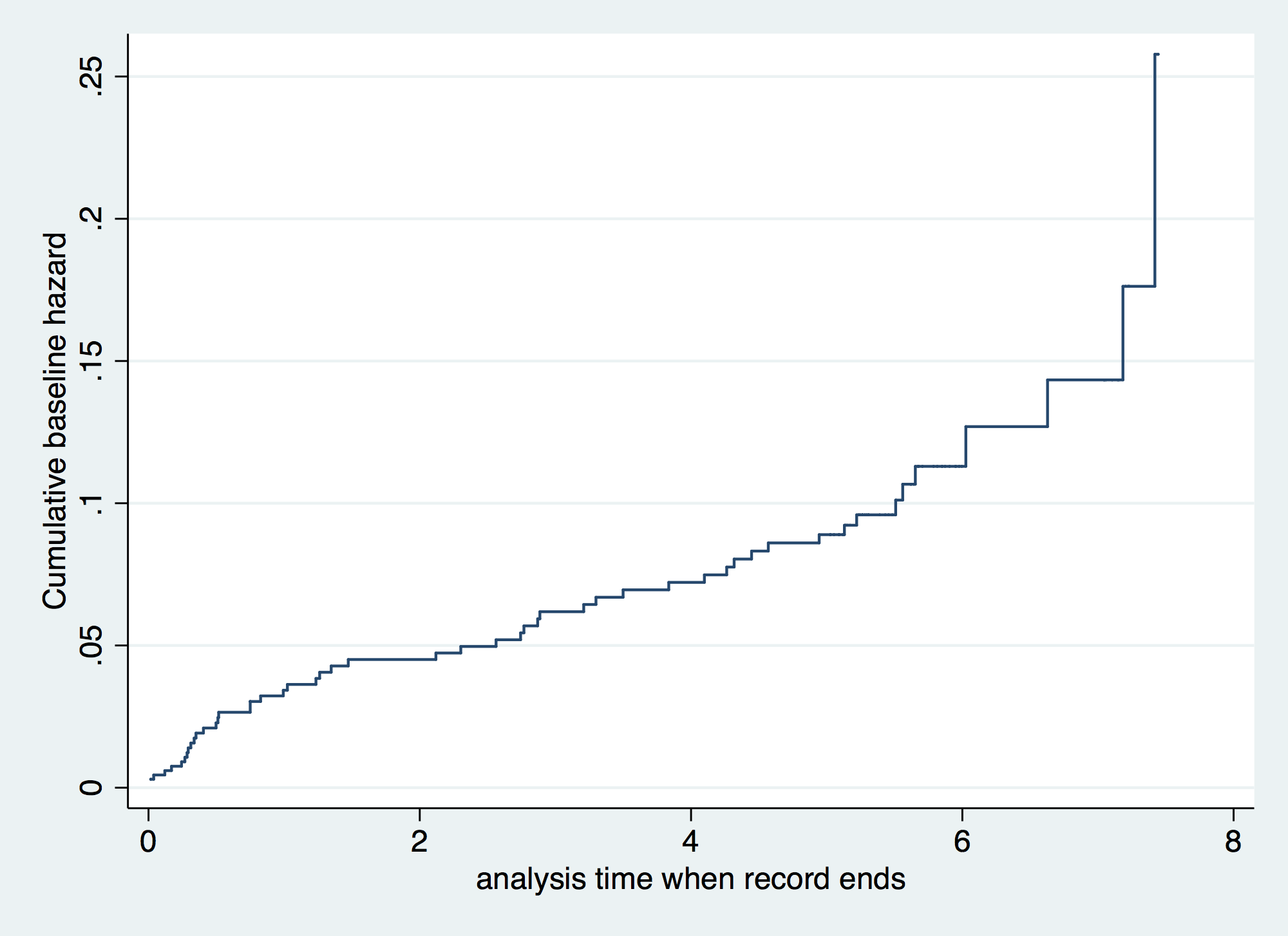
. gen H1 = H0*exp(_b[gender]) // Baseline cumulative hazard by gender . tw line H0 H1 _t, connect (J J) sort
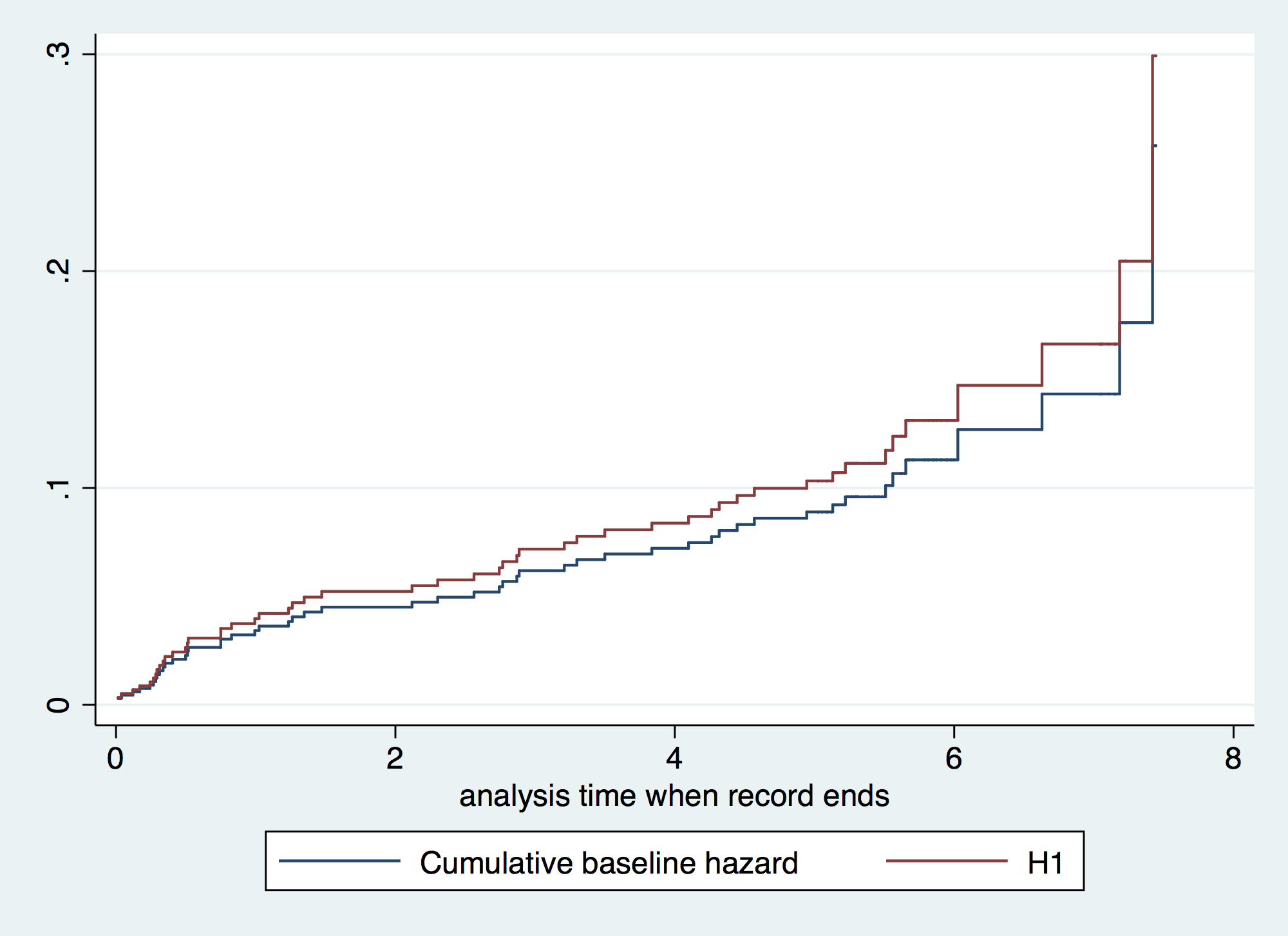
. predict S0, basesurv // Baseline Survivor function . tw line S _t, connect (J) sort
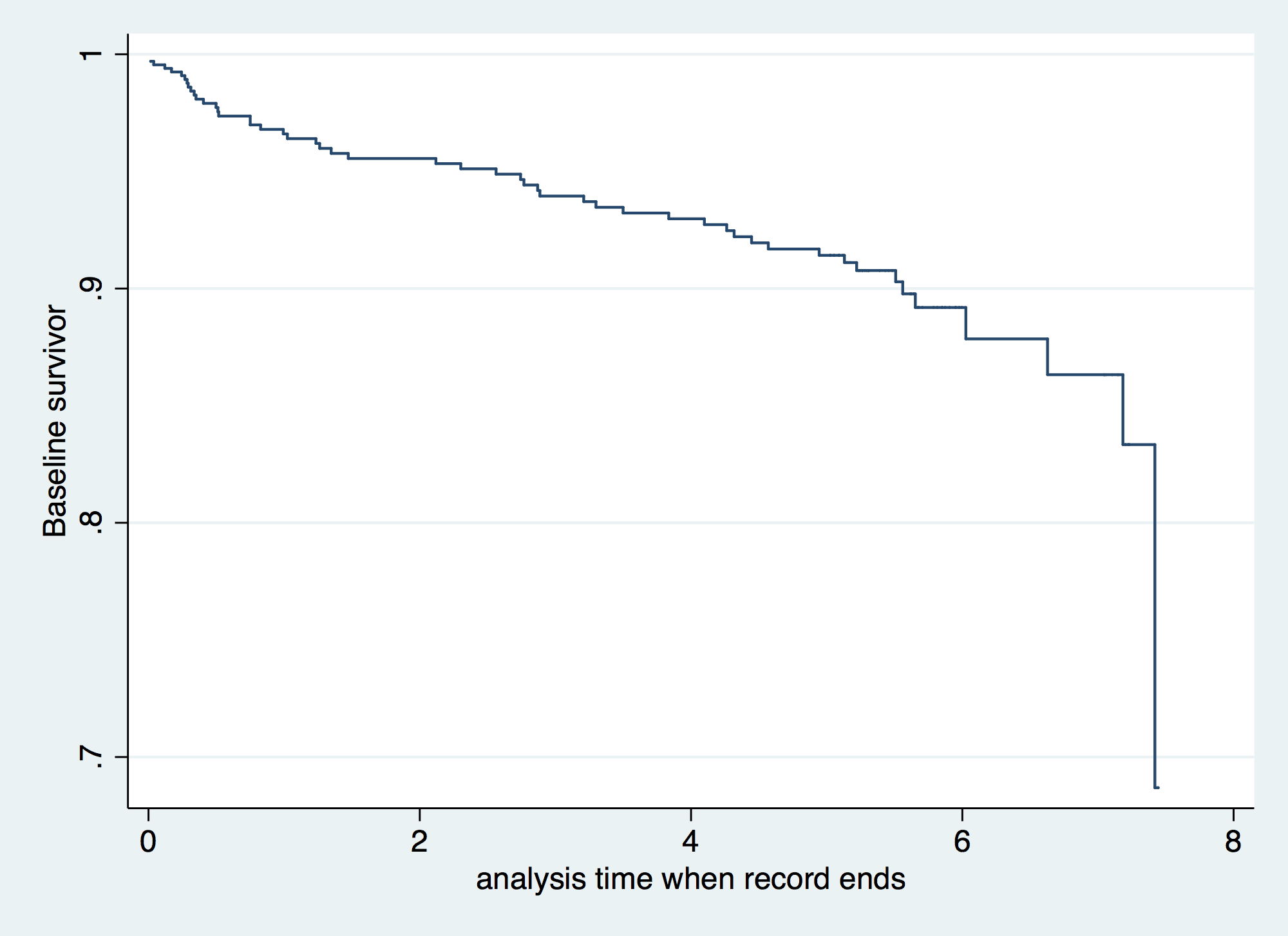
. stcox gender failure _d: folstatus == 1 analysis time _t: foltime/365.25 Iteration 0: log likelihood = -209.11972 Iteration 1: log likelihood = -207.2544 Iteration 2: log likelihood = -207.2423 Iteration 3: log likelihood = -207.2423 Refining estimates: Iteration 0: log likelihood = -207.2423 Cox regression -- Breslow method for ties No. of subjects = 100 Number of obs = 100 No. of failures = 51 Time at risk = 412.1560575 LR chi2(1) = 3.75 Log likelihood = -207.2423 Prob > chi2 = 0.0527 ------------------------------------------------------------------------------ _t | Haz. Ratio Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- gender | 1.742761 .4921308 1.97 0.049 1.002006 3.031133 ------------------------------------------------------------------------------ . stcurve, surv at1(gender =0) at2(gender =1)
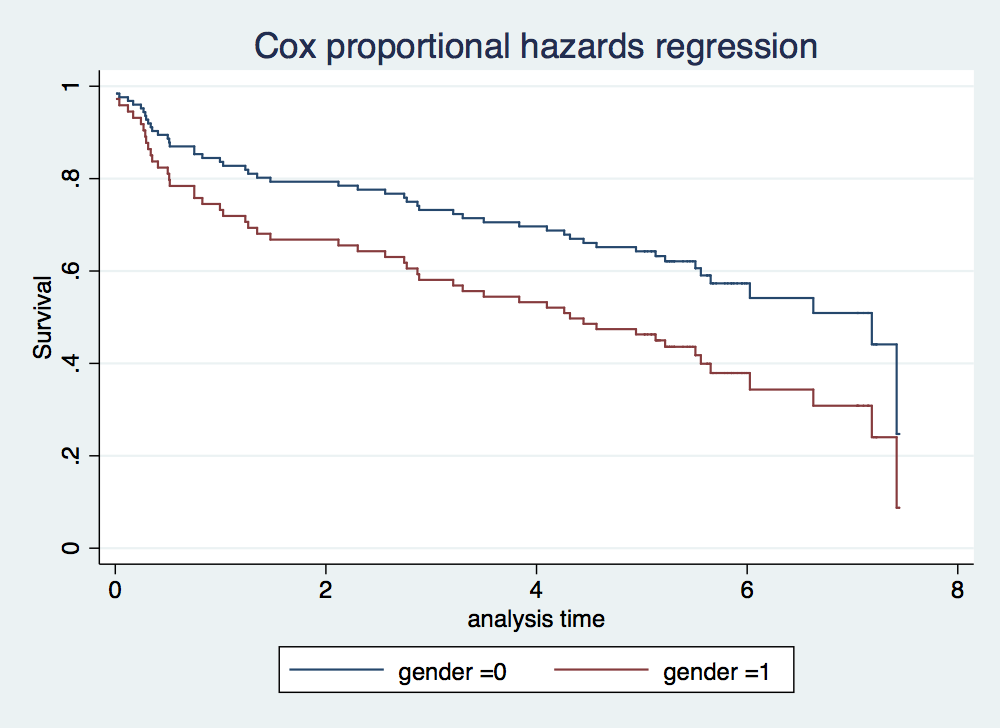
. stcox gender age failure _d: folstatus == 1 analysis time _t: foltime/365.25 Iteration 0: log likelihood = -209.11972 Iteration 1: log likelihood = -200.5215 Iteration 2: log likelihood = -200.3233 Iteration 3: log likelihood = -200.323 Refining estimates: Iteration 0: log likelihood = -200.323 Cox regression -- Breslow method for ties No. of subjects = 100 Number of obs = 100 No. of failures = 51 Time at risk = 412.1560575 LR chi2(2) = 17.59 Log likelihood = -200.323 Prob > chi2 = 0.0002 ------------------------------------------------------------------------------ _t | Haz. Ratio Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- gender | 1.16075 .351101 0.49 0.622 .6416069 2.099946 age | 1.044538 .0132085 3.45 0.001 1.018968 1.07075 ------------------------------------------------------------------------------ . stcurve, surv at1(gender =0) at2(gender =1)
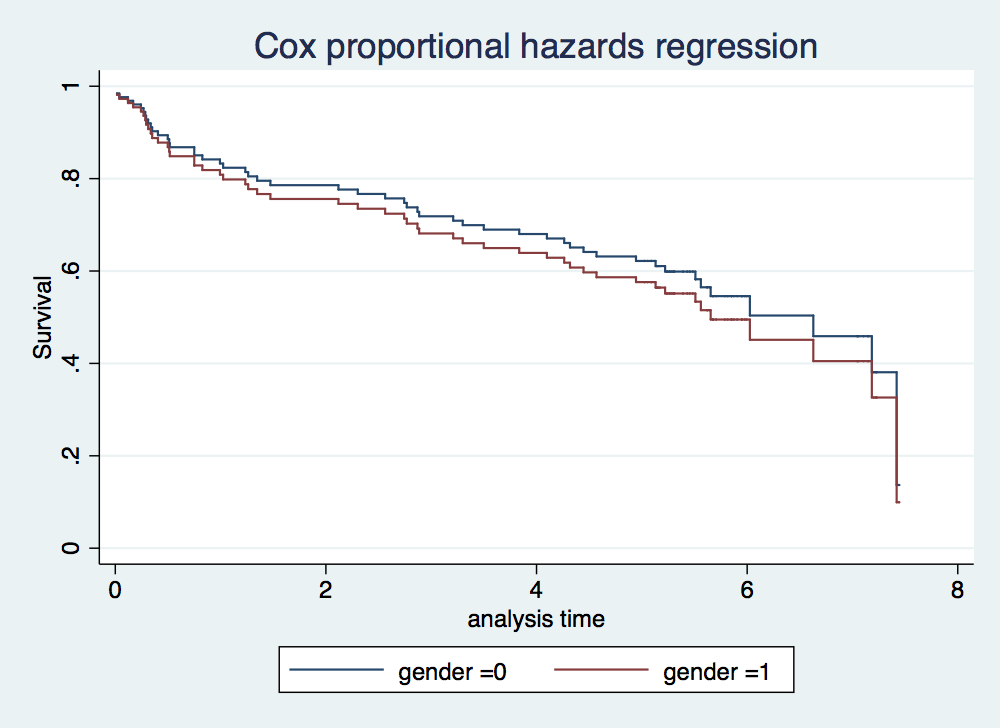
. estat phtest // There is no evidence that the model violates the proportional-hazards assump > tion Test of proportional-hazards assumption Time: Time ---------------------------------------------------------------- | chi2 df Prob>chi2 ------------+--------------------------------------------------- global test | 0.36 2 0.8353 ---------------------------------------------------------------- . estat phtest, detail Test of proportional-hazards assumption Time: Time ---------------------------------------------------------------- | rho chi2 df Prob>chi2 ------------+--------------------------------------------------- gender | -0.06680 0.27 1 0.6010 age | -0.01167 0.01 1 0.9204 ------------+--------------------------------------------------- global test | 0.36 2 0.8353 ----------------------------------------------------------------
. stphplot, by(gender) adjust(age) //Curves are roughly parallel, providing evidence in favor > of the proportional hazard assumption of gender failure _d: folstatus == 1 analysis time _t: foltime/365.25
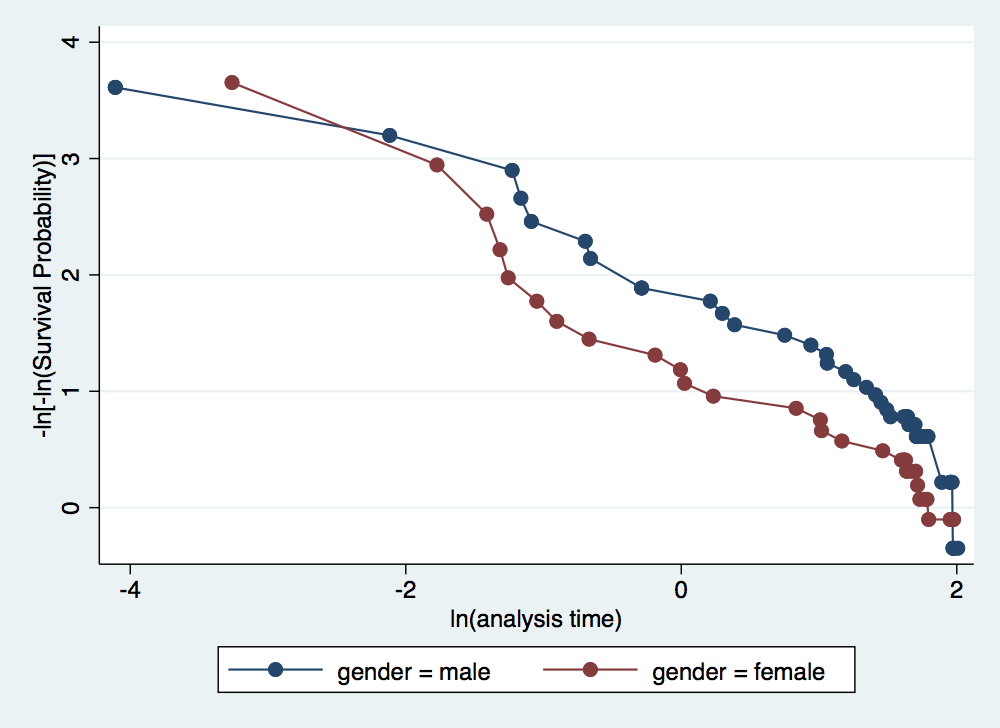
. stcox gender age failure _d: folstatus == 1 analysis time _t: foltime/365.25 Iteration 0: log likelihood = -209.11972 Iteration 1: log likelihood = -200.5215 Iteration 2: log likelihood = -200.3233 Iteration 3: log likelihood = -200.323 Refining estimates: Iteration 0: log likelihood = -200.323 Cox regression -- Breslow method for ties No. of subjects = 100 Number of obs = 100 No. of failures = 51 Time at risk = 412.1560575 LR chi2(2) = 17.59 Log likelihood = -200.323 Prob > chi2 = 0.0002 ------------------------------------------------------------------------------ _t | Haz. Ratio Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- gender | 1.16075 .351101 0.49 0.622 .6416069 2.099946 age | 1.044538 .0132085 3.45 0.001 1.018968 1.07075 ------------------------------------------------------------------------------ . stcox age, strata(gender) failure _d: folstatus == 1 analysis time _t: foltime/365.25 Iteration 0: log likelihood = -173.10245 Iteration 1: log likelihood = -166.56589 Iteration 2: log likelihood = -166.39683 Iteration 3: log likelihood = -166.3966 Refining estimates: Iteration 0: log likelihood = -166.3966 Stratified Cox regr. -- Breslow method for ties No. of subjects = 100 Number of obs = 100 No. of failures = 51 Time at risk = 412.1560575 LR chi2(1) = 13.41 Log likelihood = -166.3966 Prob > chi2 = 0.0003 ------------------------------------------------------------------------------ _t | Haz. Ratio Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- age | 1.044398 .0133473 3.40 0.001 1.018563 1.070889 ------------------------------------------------------------------------------ Stratified by gender
. hist age (bin=10, start=32, width=6)
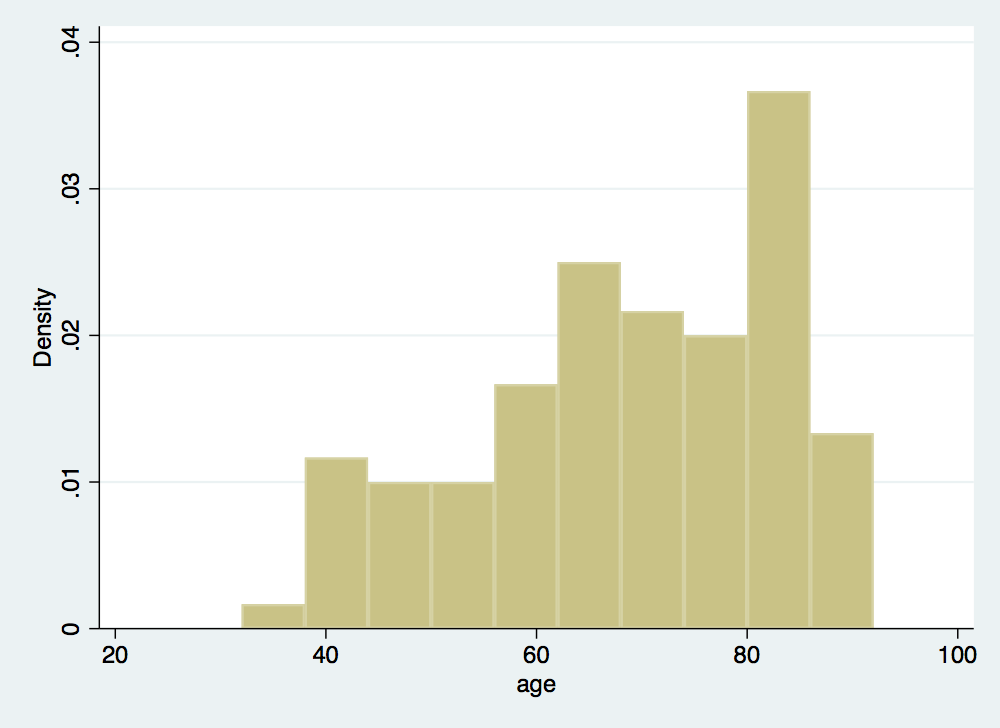
. stcox gender age failure _d: folstatus == 1 analysis time _t: foltime/365.25 Iteration 0: log likelihood = -209.11972 Iteration 1: log likelihood = -200.5215 Iteration 2: log likelihood = -200.3233 Iteration 3: log likelihood = -200.323 Refining estimates: Iteration 0: log likelihood = -200.323 Cox regression -- Breslow method for ties No. of subjects = 100 Number of obs = 100 No. of failures = 51 Time at risk = 412.1560575 LR chi2(2) = 17.59 Log likelihood = -200.323 Prob > chi2 = 0.0002 ------------------------------------------------------------------------------ _t | Haz. Ratio Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- gender | 1.16075 .351101 0.49 0.622 .6416069 2.099946 age | 1.044538 .0132085 3.45 0.001 1.018968 1.07075 ------------------------------------------------------------------------------ . predict cs, csnell //Cox-Snell residuals have a standard censored exponential distribution w > ith hazard ratio of one . stset cs, fail(folstatus) failure event: folstatus != 0 & folstatus < . obs. time interval: (0, cs] exit on or before: failure ------------------------------------------------------------------------------ 100 total observations 0 exclusions ------------------------------------------------------------------------------ 100 observations remaining, representing 51 failures in single-record/single-failure data 51 total analysis time at risk and under observation at risk from t = 0 earliest observed entry t = 0 last observed exit t = 2.761897 . sts gen Hcs = na . tw line Hcs cs cs, sort
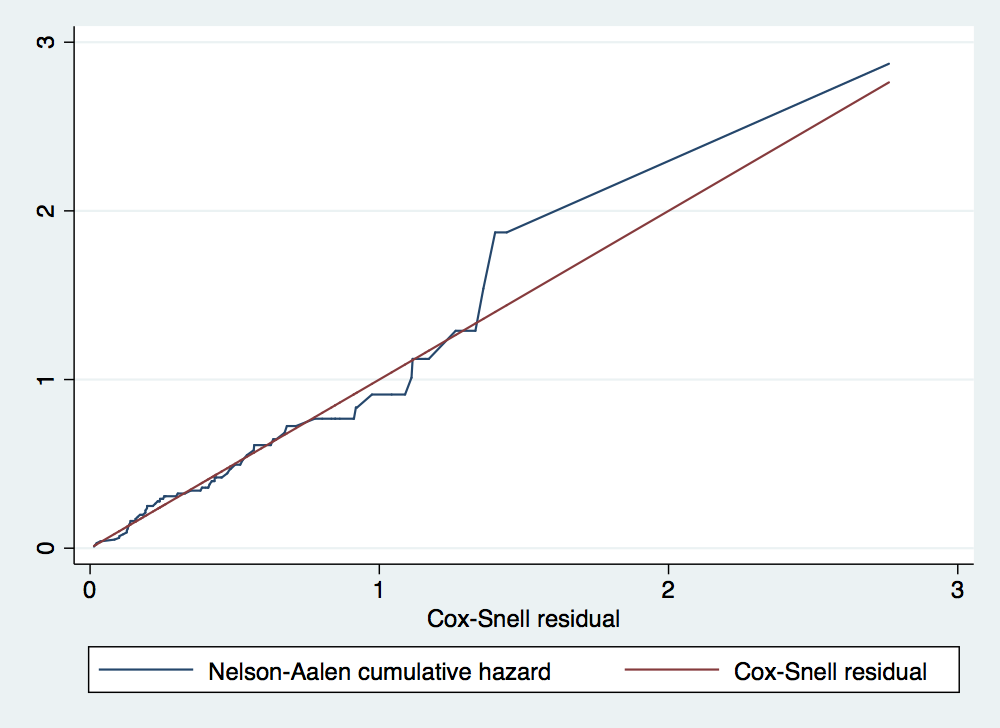
. gen lnage = ln(age) . drop Hcs cs . stcox gender lnage failure _d: folstatus analysis time _t: cs Iteration 0: log likelihood = -191.6887 Iteration 1: log likelihood = -191.65715 Iteration 2: log likelihood = -191.65714 Refining estimates: Iteration 0: log likelihood = -191.65714 Cox regression -- no ties No. of subjects = 100 Number of obs = 100 No. of failures = 51 Time at risk = 51.00000005 LR chi2(2) = 0.06 Log likelihood = -191.65714 Prob > chi2 = 0.9689 ------------------------------------------------------------------------------ _t | Haz. Ratio Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- gender | .9563769 .3030901 -0.14 0.888 .5138905 1.779867 lnage | .8683343 .730407 -0.17 0.867 .1669903 4.515258 ------------------------------------------------------------------------------ . predict cs, csnell //Cox-Snell residuals . stset cs, fail(folstatus) failure event: folstatus != 0 & folstatus < . obs. time interval: (0, cs] exit on or before: failure ------------------------------------------------------------------------------ 100 total observations 0 exclusions ------------------------------------------------------------------------------ 100 observations remaining, representing 51 failures in single-record/single-failure data 51 total analysis time at risk and under observation at risk from t = 0 earliest observed entry t = 0 last observed exit t = 2.841931 . sts gen Hcs = na . tw line Hcs cs cs, sort
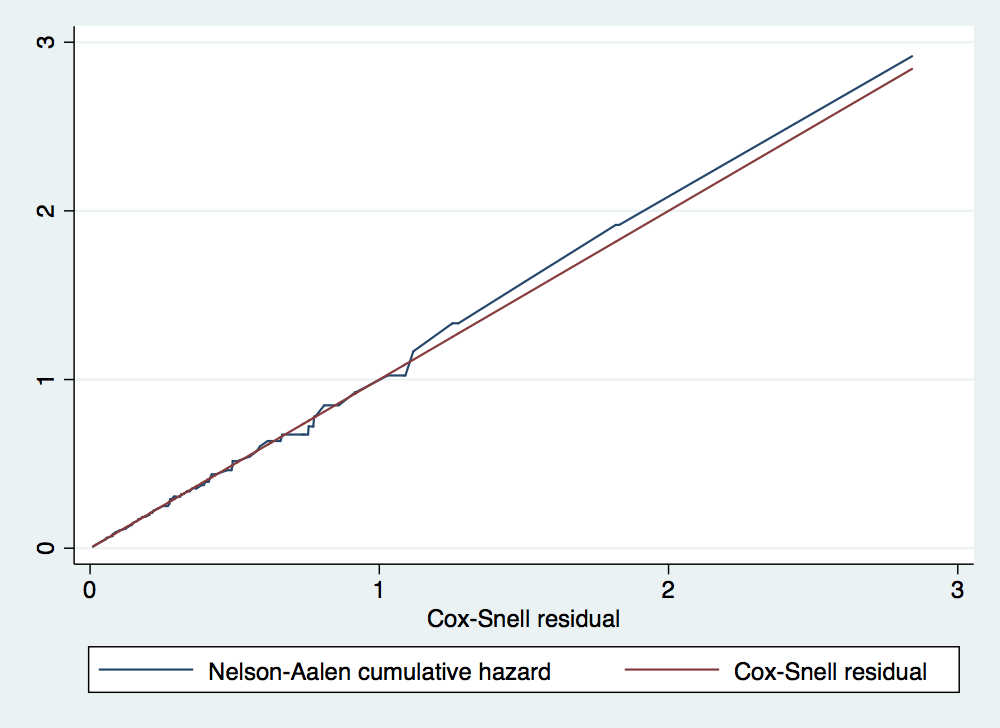
. stcox gender lnage failure _d: folstatus analysis time _t: cs Iteration 0: log likelihood = -191.44774 Iteration 1: log likelihood = -191.4413 Iteration 2: log likelihood = -191.4413 Refining estimates: Iteration 0: log likelihood = -191.4413 Cox regression -- no ties No. of subjects = 100 Number of obs = 100 No. of failures = 51 Time at risk = 51.00000025 LR chi2(2) = 0.01 Log likelihood = -191.4413 Prob > chi2 = 0.9936 ------------------------------------------------------------------------------ _t | Haz. Ratio Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- gender | .9779439 .3095562 -0.07 0.944 .5258677 1.81866 lnage | .9444136 .7887569 -0.07 0.945 .1837614 4.853668 ------------------------------------------------------------------------------ . stcurve, surv at1(gender =0) at2(gender=1)
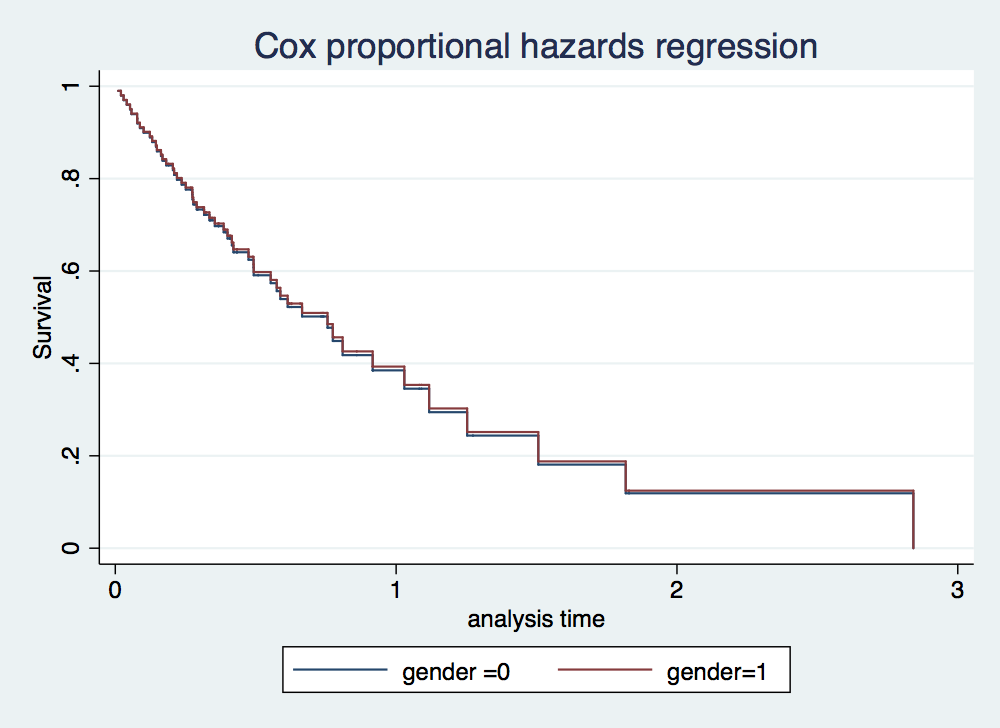
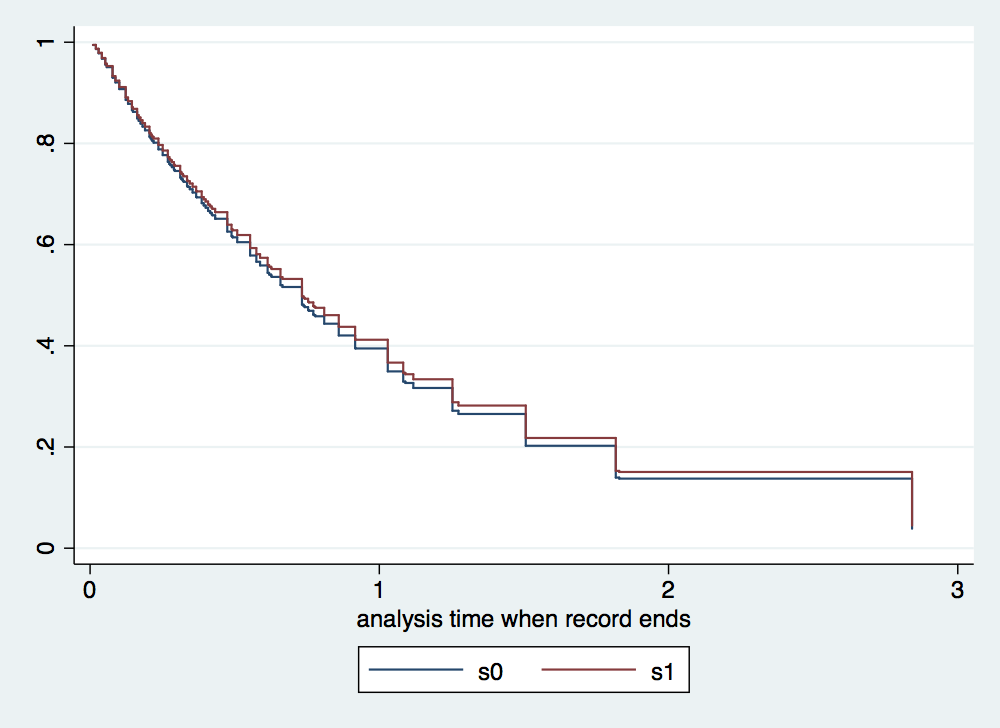
. //ssc install stpm2 . stpm2 gender age, df(3) scale(hazard) eform nolog Log likelihood = -117.47139 Number of obs = 100 ------------------------------------------------------------------------------ | exp(b) Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- xb | gender | .9540495 .3025159 -0.15 0.882 .5124679 1.776131 age | 1.000827 .0130148 0.06 0.949 .9756407 1.026663 _rcs1 | 2.738344 .3655384 7.55 0.000 2.107959 3.557246 _rcs2 | 1.04388 .1104969 0.41 0.685 .8482989 1.284553 _rcs3 | .967567 .0613668 -0.52 0.603 .8544657 1.095639 _cons | .3343509 .306433 -1.20 0.232 .0554722 2.015254 ------------------------------------------------------------------------------ Note: Estimates are transformed only in the first equation. . predict s0, meansurv at (gender 0) . predict s1, meansurv at (gender 1) . tw line s0 s1 _t, connect (J J) sort //Note different shape as we do not assume